题目内容
3．若函数y=f（x）及y=g（x）的图象分别如图所示，方程f（g（x））=0、g（f（x））=0的实根个数分别为a、b，则a+b=10．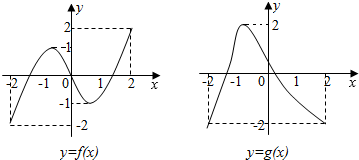
分析 结合函数图象把方程根的个数转化为函数图象的交点个数，可分别求得a，b进而可得答案．
解答 解：由图象知，f（x）=0有3个根，0，±m，1＜m＜2，
g（x）=0有2个根，-2＜n＜-1，0＜p＜1，
由f（g（x））=0，得g（x）=0或±x1，
由图象可知g（x）所对每一个值都能有2个根，因而a=6；
由g（f（x））=0，知f（x）=n 或p，
由图象可以看出n时有1根，
而p时有3个，
即b=1+3=4，
∴a+b=6+4=10，
故答案为：10．
点评 本题主要考查函数函数的图象及其应用，考查方程根的个数，利用数形结合思想是解决本题的关键．
练习册系列答案
相关题目
14．已知全集为R，集合A={x|x≤1}，B={x|x≥-2}，则A∪B=（ ）
| A． | R | B． | {x|-2≤x≤1} | C． | A | D． | B |
11．若命题p：?x0∈R，使x02+（a-1）x0+1＜0，则该命题的否定￢p为（ ）
| A． | ?x0∉R，使x02+（a-1）x0+1＜0 | B． | ?x∈R，x2+（a-1）x+1＜0 | ||
| C． | ?x0∈R，使x02+（a-1）x0+1≥0 | D． | ?x∈R，x2+（a-1）x+1≥0 |
18．
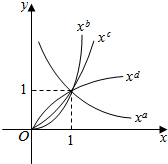幂函数y=xa，y=xb，y=xc，y=xd在第一象限的图象如图所示，则a，b，c，d的大小关系是 （ ）
幂函数y=xa，y=xb，y=xc，y=xd在第一象限的图象如图所示，则a，b，c，d的大小关系是 （ ）| A． | a＞b＞c＞d | B． | d＞b＞c＞a | C． | d＞c＞b＞a | D． | b＞c＞d＞a |
13．已知全集U={1，2，3，4，5，6，7}，A={2，4，6}，B={1，3，5}，则A∩∁UB等于（ ）
| A． | {2，5} | B． | {1，3，5} | C． | {2，4，5} | D． | {2，4，6} |