13.先后抛掷两枚均匀的正方体骰子(它们的六个面分别标有点数1、2、3、4、5、6),骰子朝上的面的点数分别为x,y,则logxy=1的概率为( )
| A. | $\frac{1}{6}$ | B. | $\frac{1}{12}$ | C. | $\frac{5}{36}$ | D. | $\frac{1}{2}$ |
11.有命题m:“?x0∈(0,$\frac{1}{3}$),($\frac{1}{2}$)${\;}^{{x}_{0}}$<log${\;}_{\frac{1}{3}}$x0”,n:“?x0∈(0,+∞),($\frac{1}{2}$)${\;}^{{x}_{0}}$=log${\;}_{\frac{1}{3}}$x0>x0”,则在命题p1:m∨n,p2:m∧n,p3:(¬m)∨n和p4:m∧(¬n)中,真命题是( )
| A. | p1,p2,p3 | B. | p2,p3,p4 | C. | p1,p3 | D. | p2,p4 |
10.已知角α的终边经过点(-3,4),则$sin({α+\frac{π}{4}})$的值( )
| A. | $\frac{\sqrt{2}}{5}$ | B. | -$\frac{\sqrt{2}}{5}$ | C. | $\frac{\sqrt{2}}{10}$ | D. | -$\frac{\sqrt{2}}{10}$ |
9.抛物线$y=-\frac{1}{8}{x^2}$的焦点坐标及准线方程分别为( )
| A. | (0,-2),x=2 | B. | (0,-2),y=2 | C. | (2,0),x=-2 | D. | (2,0),y=-2 |
6.函数y=$tan(2x-\frac{π}{4})$的其中一个对称中心为( )
0 250597 250605 250611 250615 250621 250623 250627 250633 250635 250641 250647 250651 250653 250657 250663 250665 250671 250675 250677 250681 250683 250687 250689 250691 250692 250693 250695 250696 250697 250699 250701 250705 250707 250711 250713 250717 250723 250725 250731 250735 250737 250741 250747 250753 250755 250761 250765 250767 250773 250777 250783 250791 266669
| A. | $(-\frac{π}{8},0)$ | B. | $(\frac{π}{2},0)$ | C. | (0,0) | D. | $(\frac{π}{4},0)$ |
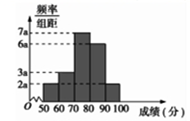 20名学生某次数学考试成绩(单位:分)的频率分布直方图如下:
20名学生某次数学考试成绩(单位:分)的频率分布直方图如下: