17.已知函数f(x)=sin(2x+φ),其中φ为实数,若$f(x)≤|{f(\frac{π}{3})}|$对于任意x∈R恒成立,且$f(\frac{π}{2})>f(π)$,则$f(\frac{5π}{12})$的值为( )
| A. | $-\frac{{\sqrt{3}}}{2}$ | B. | 0 | C. | $\frac{1}{2}$ | D. | $\frac{{\sqrt{3}}}{2}$ |
16.下列结论正确的是( )
| A. | 若a<b,则2a<2b | B. | 若a>b,则a2>b2 | C. | 若a<b,则$\sqrt{a}<\sqrt{b}$ | D. | 若a>b,则ac2>bc2 |
8.将函数y=sin($\frac{1}{2}x$+$\frac{π}{3}$)的图象作怎样的变换可得到y=sinx的图象( )
0 250438 250446 250452 250456 250462 250464 250468 250474 250476 250482 250488 250492 250494 250498 250504 250506 250512 250516 250518 250522 250524 250528 250530 250532 250533 250534 250536 250537 250538 250540 250542 250546 250548 250552 250554 250558 250564 250566 250572 250576 250578 250582 250588 250594 250596 250602 250606 250608 250614 250618 250624 250632 266669
| A. | 将y=sin($\frac{1}{2}x+\frac{π}{3}$)的图象向右平移$\frac{2π}{3}$个单位,再将所得图象所得点的横坐标变为原来的$\frac{1}{2}$ | |
| B. | 将y=sin($\frac{1}{2}x+\frac{π}{3}$)的图象向右平移$\frac{π}{3}$个单位,再将所得图象所得点的横坐标变为原来的$\frac{1}{2}$ | |
| C. | 将y=sin($\frac{1}{2}x+\frac{π}{3}$)的图象所有点的横坐标变为原来的2倍,再将所得图象向右平移$\frac{π}{3}$个单位 | |
| D. | 将y=sin($\frac{1}{2}x+\frac{π}{3}$)的图象所有点的横坐标变为原来的$\frac{1}{2}$倍,再将所得图象向右平移$\frac{2π}{3}$个单位 |
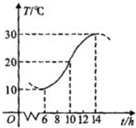 如图,某地一天从6~14时的温度变化,曲线近似满足函数y=Asin(?x+φ)+b,(A>0,?>0,φ∈(0,2π)),试求这段曲线的函数解析式.
如图,某地一天从6~14时的温度变化,曲线近似满足函数y=Asin(?x+φ)+b,(A>0,?>0,φ∈(0,2π)),试求这段曲线的函数解析式.