设f(x)=|lg$\sqrt{x}$|+|lg2$\sqrt{x}$|．.求g(x)并作图,的最小值,=$\frac{1}{2}$的解集．题目和参考答案——青夏教育精英家教网—

题目内容

13．设f（x）=|lg$\sqrt{x}$|+|lg2$\sqrt{x}$|．
（1）若f（x）=lg g（x），求g（x）并作图；
（2）求f（x）的最小值；
（3）求方程f（x）=$\frac{1}{2}$的解集．

分析（1）分类讨论得出当0＜x≤$\frac{1}{4}$时，f（x）=-lg$\sqrt{x}$-lg2$\sqrt{x}$=-lg2x，当$\frac{1}{4}$＜x≤1时，f（x）=-lg$\sqrt{x}$+lg2$\sqrt{x}$=lg2，运用分段函数写出即可；
（2）根据g（x）的图象判断得出g（x）的最小值为2，利用复合函数求解f（x）=lgg（x）的最小值为lg2；
（3）分段求解即可当0$＜x≤\frac{1}{4}$，$\frac{1}{2x}$=$\sqrt{10}$，x=$\frac{\sqrt{10}}{20}$，当x≥1时，2x=$\sqrt{10}$，x=$\frac{\sqrt{10}}{2}$

解答解：（1）∵f（x）=|lg$\sqrt{x}$|+|lg2$\sqrt{x}$|．
∴当0＜x≤$\frac{1}{4}$时，f（x）=-lg$\sqrt{x}$-lg2$\sqrt{x}$=-lg2x，
当$\frac{1}{4}$＜x≤1时，f（x）=-lg$\sqrt{x}$+lg2$\sqrt{x}$=lg2，
当x＞1时，f（x）=lg$\sqrt{x}$+lg2$\sqrt{x}$=lg2x，
∴f（x）=$\left\{\begin{array}{l}{-lg2x，0＜x≤\frac{1}{4}}\\{lg2，\frac{1}{4}＜x＜1}\\{lg2x，x≥1}\end{array}\right.$
即g（x）=$\left\{\begin{array}{l}{\frac{1}{2x}，0＜x≤\frac{1}{4}}\\{2，\frac{1}{4}＜x＜1}\\{2x，x≥1}\end{array}\right.$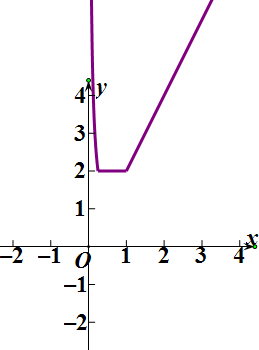

（2）g（x）的最小值为2，故f（x）=lgg（x）的最小值为lg2；
（3）方程f（x）=$\frac{1}{2}$即g（x）=$\sqrt{10}$，
∵当0$＜x≤\frac{1}{4}$，$\frac{1}{2x}$=$\sqrt{10}$，x=$\frac{\sqrt{10}}{20}$，
当x≥1时，2x=$\sqrt{10}$，x=$\frac{\sqrt{10}}{2}$
∴方程f（x）=$\frac{1}{2}$的解集{$\frac{\sqrt{10}}{20}$，$\frac{\sqrt{10}}{2}$}

点评本题考查了分类讨论，数形结合的思想，对数的性质，化简计算能力，属于综合题目，但是难度不大．

练习册系列答案

相关题目

a²＜b²

${（{\frac{1}{2}}）^a}＜{（{\frac{1}{2}}）^b}$

D．

$\frac{b}{a}+\frac{a}{b}$＞2

4．设x＞0，那么3-$\frac{1}{x}$-x有（　　）

1．已知A、B、C是△ABC的三个内角，f（x）=cos2x+$\frac{5}{2}$sinAsinx，（x∈R），sin（A+$\frac{π}{4}$）=$\frac{7\sqrt{2}}{10}$，A∈（$\frac{π}{4}$，$\frac{π}{2}$）．
（1）求函数f（x）的值域；
（2）若f（x）_max=f（B），且AC=5，求△ABC的面积．

8．将函数y=sin（$\frac{1}{2}x$+$\frac{π}{3}$）的图象作怎样的变换可得到y=sinx的图象（　　）

	A．	将y=sin（$\frac{1}{2}x+\frac{π}{3}$）的图象向右平移$\frac{2π}{3}$个单位，再将所得图象所得点的横坐标变为原来的$\frac{1}{2}$
	B．	将y=sin（$\frac{1}{2}x+\frac{π}{3}$）的图象向右平移$\frac{π}{3}$个单位，再将所得图象所得点的横坐标变为原来的$\frac{1}{2}$
	C．	将y=sin（$\frac{1}{2}x+\frac{π}{3}$）的图象所有点的横坐标变为原来的2倍，再将所得图象向右平移$\frac{π}{3}$个单位
	D．	将y=sin（$\frac{1}{2}x+\frac{π}{3}$）的图象所有点的横坐标变为原来的$\frac{1}{2}$倍，再将所得图象向右平移$\frac{2π}{3}$个单位