18．已知O是△ABC所在平面内一点.且满足($\overrightarrow{OB}$-$\overrightarrow{OC}$)•($\overrightarrow{OB}$+$\o——青夏教育精英家教网——

18．已知O是△ABC所在平面内一点，且满足（$\overrightarrow{OB}$-$\overrightarrow{OC}$）•（$\overrightarrow{OB}$+$\overrightarrow{OC}$-2$\overrightarrow{OA}$）=0，判断△ABC是哪类三角形．

17．数列{a_n}中，有a₁=1，a_n+1=$\frac{1}{3}$S_n，（n∈N^*），求：
（1）数列{a_n}的通项公式；
（2）a₂+a₄+a₆+…+a_2n的值．

16．已知数列{a_n}满足：a₁=1，a_n+1=$\frac{{a}_{n}+3}{{a}_{n}+1}$（n=1，2，3…）
（1）设b_n=|a_n-$\sqrt{3}$|，证明：b_n+1＜b_n；
（2）证明：b₁+b₂+…+b_n＜$\sqrt{3}$+1．

15．设各项均为正数的等比数列{a_n}的公比为q，[a_n]表示不超过实数a_n的最大整数（如[1.2]=1），设b_n=[a_n]，数列{b_n}的前n项和为T_n，{a_n}的前n项和为S_n，
（1）若a₁=4，q=$\frac{1}{2}$，求S_n及T_n；
（2）若对于任意不超过2015的正整数n，都有T_n=2n+1，证明：（$\frac{2}{3}$）${\;}^{\frac{1}{2013}}$＜q＜1．

14．设向量$\overrightarrow{i}$=（1，0），$\overrightarrow{j}$=（0，1），动点P（x，y），记向量$\overrightarrow{a}$=（x+m）$\overrightarrow{i}$+y$\overrightarrow{j}$，$\overrightarrow{b}$=（x-m）$\overrightarrow{i}$+y$\overrightarrow{j}$，且|$\overrightarrow{a}$|+|$\overrightarrow{b}$|=6，这里m为常数，且0＜m＜3，x≥0，y∈R．
（1）求动点P（x，y）的轨迹方程；
（2）当m=2时，设Q（1，0），求|PQ|的最大值和最小值；
（3）已知点A（-1，0），直线l：y=$\frac{1}{3}$（x-1）与点P的轨迹交于M、N两点，问是否存在实数m，使得$\overrightarrow{AM}$•$\overrightarrow{AN}$=$\frac{26}{9}$？若存在，求出所有满足条件的m的值；若不存在，请说明理由．

13．在△ABC中，已知A（cosx，sinx），（0≤x≤2π），B（1，1），顶点C满足$\overrightarrow{OA}+\overrightarrow{OB}=\overrightarrow{OC}$，设f（x）=|$\overrightarrow{OC}$|²
（1）求f（x）的对称轴，对称中心；
（2）若f（C）=3+$\sqrt{6}$，求cosC．

12．已知向量$\overrightarrow{a}$=（1，$\sqrt{3}$sinωx），$\overrightarrow{b}$=（cos²ωx-1，cosωx）（ω＞0），设函数f（x）=$\overrightarrow{a}•\overrightarrow{b}$的最小正周期为π
（1）求ω的值；
（2）求函数f（x）在[0，$\frac{2}{3}$]上的值域．

11．已知函数f（x）=x²+mx+n的图象过点（1，3），且f（-1+x）=f（-1-x）对任意实数都成立，函数y=g（x）与y=f（x）的图象关于原点对称．
（1）求f（x）与g（x）的解析式；
（2）若F（x）=g（x）-λf（x）在[-1，1]上是增函数，求实数λ的取值范围．

10．已知$\overrightarrow{m}$=（$\sqrt{3}$sin2x+2，cosx），$\overrightarrow{n}$=（1，2cosx），设f（x）=$\overrightarrow{m}$•$\overrightarrow{n}$．
（1）求f（x）的最小正周期及最值；
（2）在△ABC中，若f（A）=4，b=1，S_△ABC=$\frac{\sqrt{3}}{2}$，求a的值．

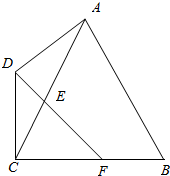如图所示，平面四边形ABCD中，AB=AC=BC=$\sqrt{3}$，CD=AD=1，已知$\overrightarrow{AE}$=$λ\overrightarrow{AC}$，$\overrightarrow{CF}$=λ$\overrightarrow{CB}$，λ∈（0，1），且存在实数t使$\overrightarrow{CE}$=t$\overrightarrow{CD}$+（1-t）$\overrightarrow{CF}$，则$\overrightarrow{EA}$•$\overrightarrow{AB}$=（　　）

$\frac{\sqrt{3}}{2}$

-$\frac{\sqrt{3}}{2}$

0 249351 249359 249365 249369 249375 249377 249381 249387 249389 249395 249401 249405 249407 249411 249417 249419 249425 249429 249431 249435 249437 249441 249443 249445 249446 249447 249449 249450 249451 249453 249455 249459 249461 249465 249467 249471 249477 249479 249485 249489 249491 249495 249501 249507 249509 249515 249519 249521 249527 249531 249537 249545 266669