4.已知定义在R上的函数f(x),g(x)满足$\frac{f(x)}{g(x)}={b^x}$,且f′(x)g(x)<f(x)g′(x),$\frac{f(1)}{g(1)}+\frac{{f({-1})}}{{g({-1})}}=\frac{5}{2}$,若{an}是正项等比数列,且a5a7+2a6a8+a4a12=$\frac{f(4)}{g(4)}$,则a6+a8等于( )
| A. | $\frac{1}{2}$ | B. | $\frac{1}{4}$ | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
3.已知命题p:“直线l垂直于平面α内的无数条直线”的充要条件是“l⊥α”;命题q:若平面α⊥平面β,直线a?β,则“a⊥α”是“a平行于β”的充分不必要条件,则正确命题是( )
| A. | p∧q | B. | (¬p)∧q | C. | (?p)∧(¬q) | D. | p∨(¬q) |
2.已知实数x,y满足$\left\{\begin{array}{l}2x-y≤0\\ x-3y+5≥0\\ x>0\\ y>0\end{array}$,则$z={({\frac{1}{4}})^x}•{({\frac{1}{2}})^y}$的最小值为( )
| A. | 4 | B. | 2 | C. | $\frac{1}{8}$ | D. | $\frac{1}{16}$ |
1.设i是虚数单位,复数$\frac{5}{2-i}$的虚部为( )
| A. | -i | B. | -1 | C. | i | D. | 1 |
16.已知,x,y∈R,则“|x+y|=|x|+|y|”是“xy>0”的( )
0 248470 248478 248484 248488 248494 248496 248500 248506 248508 248514 248520 248524 248526 248530 248536 248538 248544 248548 248550 248554 248556 248560 248562 248564 248565 248566 248568 248569 248570 248572 248574 248578 248580 248584 248586 248590 248596 248598 248604 248608 248610 248614 248620 248626 248628 248634 248638 248640 248646 248650 248656 248664 266669
| A. | 充分不必要条件 | B. | 必要不充分条件 | ||
| C. | 充要条件 | D. | 既不充分也不必要条件 |
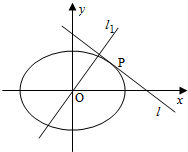 已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.
已知椭圆C:$\frac{{x}^{2}}{{a}^{2}}+\frac{{y}^{2}}{{b}^{2}}=1$(a>b>0)的离心率为$\frac{1}{2}$,顺次连接其四个顶点构成的四边形的面积为4$\sqrt{3}$.