19．${∫} {0}^{π}$dx=．——青夏教育精英家教网——

19．${∫}_{0}^{π}$（x+cosx）dx=．

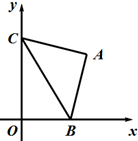如图所示，在平面直角坐标系xOy中，点B，C分别在x轴和y轴非负半轴上，点A在第一象限，且∠BAC=90°，AB=AC=4，那么O，A两点间距离的（　　）

	A．	最大值是$4\sqrt{2}$，最小值是4		B．	最大值是8，最小值是4
	C．	最大值是$4\sqrt{2}$，最小值是2		D．	最大值是8，最小值是2

17．将函数$y=cos（\frac{1}{2}x-\frac{π}{6}）$图象向左平移$\frac{π}{3}$个长度单位，再把所得图象上各点的横坐标缩短到原来的一半（纵坐标不变），所得图象的函数解析式是（　　）

$y=cos（x+\frac{π}{6}）$

$y=cos\frac{1}{4}x$

$y=cos（\frac{1}{4}x-\frac{π}{3}）$

16．已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1（a＞0，b＞0）$的一条渐近线方程是$y=\sqrt{3}x$，它的一个焦点坐标为（2，0），则双曲线的方程为（　　）

$\frac{x^2}{2}-\frac{y^2}{6}=1$

$\frac{x^2}{6}-\frac{y^2}{2}=1$

${x^2}-\frac{y^2}{3}=1$

$\frac{x^2}{3}-{y^2}=1$

15．在等比数列{a_n}中，a₃+a₄=4，a₂=2，则公比q等于（　　）

14．在复平面内，复数$\frac{7+i}{3+4i}$对应的点的坐标为（　　）

$（\frac{17}{25}，-1）$

$（\frac{17}{5}，-1）$

13．已知函数f（x）=lnx-ax+1，a是常数，a∈R．
（Ⅰ）求曲线y=f（x）在点P（1，f（1））处的切线l的方程；
（Ⅱ）求函数f（x）的单调区间；
（Ⅲ）证明：函数f（x）（x≠1）的图象在直线l的下方．

如图，四棱锥E-ABCD中，侧面EAB⊥底面ABCD，底面ABCD是直角梯形，
AD∥BC，AB=BC=2AD，∠DAB=90°，△EAB是正三角形，F为EC的中点．
（Ⅰ）求证：DF∥平面EAB；
（Ⅱ）求证：DF⊥平面EBC．

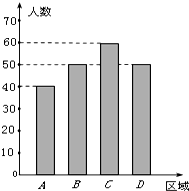教育资源的不均衡是促进“择校热”的主要因素之一，“择校热”也是教育行政部门一直着力解决的问题．某社会调查机构为了调查学生家长对解决“择校热”的满意程度，从A，B，C，D四个不同区域内分别选择一部分学生家长作调查，每个区域选出的人数如条形图所示．为了了解学生家长的满意程度，对每位家长都进行了问卷调查，然后用分层抽样的方法从调查问卷中抽取20份进行统计，统计结果如下面表格所示：

	满意	一般	不满意
A区域	50%	25%	25%
B区域	80%	0	20%
C区域	50%	50%	0
D区域	40%	20%	40%

（Ⅰ）若家长甲来自A区域，求家长甲的调查问卷被选中的概率；
（Ⅱ）若想从调查问卷被选中且填写不满意的家长中再选出2人进行面谈，求这2人中至少有一人来自D区域的概率．

已知函数$f（x）=Asin（ωx+ϕ）（A＞0，ω＞0，|ϕ|＜\frac{π}{2}）$的图象的一部分如图所示．
（Ⅰ）求函数f（x）的解析式；
（Ⅱ）当$x∈[-6，-\frac{1}{3}]$时，求函数y=f（x）的最大值与最小值及相应的x的值．

0 245007 245015 245021 245025 245031 245033 245037 245043 245045 245051 245057 245061 245063 245067 245073 245075 245081 245085 245087 245091 245093 245097 245099 245101 245102 245103 245105 245106 245107 245109 245111 245115 245117 245121 245123 245127 245133 245135 245141 245145 245147 245151 245157 245163 245165 245171 245175 245177 245183 245187 245193 245201 266669