题目内容
11.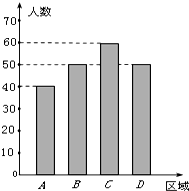 教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:
教育资源的不均衡是促进“择校热”的主要因素之一,“择校热”也是教育行政部门一直着力解决的问题.某社会调查机构为了调查学生家长对解决“择校热”的满意程度,从A,B,C,D四个不同区域内分别选择一部分学生家长作调查,每个区域选出的人数如条形图所示.为了了解学生家长的满意程度,对每位家长都进行了问卷调查,然后用分层抽样的方法从调查问卷中抽取20份进行统计,统计结果如下面表格所示:| 满意 | 一般 | 不满意 | |
| A区域 | 50% | 25% | 25% |
| B区域 | 80% | 0 | 20% |
| C区域 | 50% | 50% | 0 |
| D区域 | 40% | 20% | 40% |
(Ⅱ)若想从调查问卷被选中且填写不满意的家长中再选出2人进行面谈,求这2人中至少有一人来自D区域的概率.
分析 (Ⅰ)通过频率分布直方图,来自A区域的家长为40人,通过分层抽样可得从A区域的家长问卷中抽取的数目,然后求解概率.
(II)设事件N=“从填写不满意的家长中选出2人,至少有一人来自区域D”从填写不满意的学生中选出2人的基本事件个数,而事件N的个数,然后求解概率.
解答 (本小题共13分)
解:(Ⅰ)由条形图可得,来自A,B,C,D四个区域的家长共有200人,…(1分)
其中来自A区域的家长为40人,…(2分)
由分层抽样可得从A区域的家长问卷中抽取了 $20×\frac{40}{200}=4$份.…(4分)
设事件M=“家长甲被选中进行问卷调查”,…(5分)
则$P(M)=\frac{4}{40}=0.1$.…(6分)
(II) 由图表可知,来自A,B,C,D四区域的家长分别接受调查的人数为4,5,6,5.
其中不满意的家长人数分别为1,1,0,2个.…(7分)
记来自A区域不满意的家长是a;来自B区域不满意的家长是b;
来自D区域不满意的家长是c,d.…(8分)
设事件N=“从填写不满意的家长中选出2人,至少有一人来自区域D”…(9分)
从填写不满意的学生中选出2人,共有:(a,b),(a,c),(a,d),(b,c),(b,d),(c,d)6个基本事件,…(10分)
而事件N有(a,c),(a,d),(b,c),(b,d),(c,d)5个基本事件,…(11分)
故$P(N)=\frac{5}{6}$.…(13分)
点评 本题考查分层抽样,频率分布直方图以及古典概型的概率的求法,基本知识的考查.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的一条渐近线方程是$y=\sqrt{3}x$,它的一个焦点坐标为(2,0),则双曲线的方程为( )
| A. | $\frac{x^2}{2}-\frac{y^2}{6}=1$ | B. | $\frac{x^2}{6}-\frac{y^2}{2}=1$ | C. | ${x^2}-\frac{y^2}{3}=1$ | D. | $\frac{x^2}{3}-{y^2}=1$ |
20.已知a,b,c∈R,那么下列命题中正确的是( )
| A. | 若a<b,则ac2<bc2 | B. | 若a>b>0,c<0,则$\frac{c}{a}<\frac{c}{b}$ | ||
| C. | 若a>b,则(a+c)2>(b+c)2 | D. | 若ab>0,则$\frac{a}{b}+\frac{b}{a}≥2$ |