题目内容
12．
如图，四棱锥E-ABCD中，侧面EAB⊥底面ABCD，底面ABCD是直角梯形，AD∥BC，AB=BC=2AD，∠DAB=90°，△EAB是正三角形，F为EC的中点．
（Ⅰ）求证：DF∥平面EAB；
（Ⅱ）求证：DF⊥平面EBC．
分析 （I）设M为BE的中点，连结FM，AM，可证四边形AMFD是平行四边形，既有AM∥DF，又DF?平面EAB，AM?平面EAB，即可证明DF∥平面EAB．
（II）先证明BC⊥AB，可证BC⊥平面EAB，BC⊥AM，又BE⊥AM，从而可证AM⊥平面EBC，由AM∥DF，即可证明DF⊥平面EBC．
解答 （本小题共14分）
证明：（I）设M为BE的中点，连结FM，AM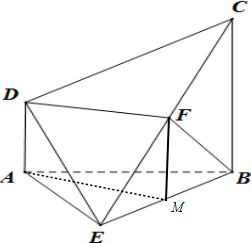
∵F为EC的中点
∴FM∥BC，FM=$\frac{1}{2}$BC
∵AD∥BC，BC=2AD
∴四边形AMFD是平行四边形
∴AM∥DF …（6分）
又DF?平面EAB，AM?平面EAB
∴DF∥平面EAB
（II）∵AD∥BC，∠DAB=90°
∴BC⊥AB
又侧面EAB⊥底面ABCD，侧面EAB∩底面ABCD=AB，AB?平面ABCD
∴BC⊥平面EAB，又AM?平面EAB
∴BC⊥AM
∵△EAB是正三角形，F为EC的中点
∴BE⊥AM
又BC∩BE=B，BC?平面EBC，BE?平面EBC
∴AM⊥平面EBC
∵AM∥DF
∴DF⊥平面EBC …（14分）
点评 本题主要考查了直线与平面垂直的判定，直线与平面平行的判定，考查了空间想象能力和转化思想，属于基本知识的考查．
练习册系列答案
名校课堂系列答案
相关题目
甲、乙两个小组各有10名学生，他们的某次数学测试成绩的茎叶图如图所示．现从这20名学生中随机抽取一名，则这名学生来自甲小组且成绩不低于85分的概率是$\frac{1}{4}$．
17．将函数$y=cos（\frac{1}{2}x-\frac{π}{6}）$图象向左平移$\frac{π}{3}$个长度单位，再把所得图象上各点的横坐标缩短到原来的一半（纵坐标不变），所得图象的函数解析式是（ ）
| A． | $y=cos（x+\frac{π}{6}）$ | B． | $y=cos\frac{1}{4}x$ | C． | y=cosx | D． | $y=cos（\frac{1}{4}x-\frac{π}{3}）$ |
4．甲、乙两人为了响应政府“节能减排”的号召，决定各购置一辆纯电动汽车．经了解目前市场上销售的主流纯电动汽车，按续驶里程数R（单位：公里）可分为三类车型，A：80≤R＜150，B：150≤R＜250，C：R≥250．甲从A，B，C三类车型中挑选，乙从B，C两类车型中挑选，甲、乙二人选择各类车型的概率如下表：
若甲、乙都选C类车型的概率为$\frac{3}{10}$．
（Ⅰ）求p，q的值；
（Ⅱ）求甲、乙选择不同车型的概率；
（Ⅲ）某市对购买纯电动汽车进行补贴，补贴标准如下表：
记甲、乙两人购车所获得的财政补贴和为X，求X的分布列．
| 车型 概率 人 | A | B | C |
| 甲 | $\frac{1}{5}$ | p | q |
| 乙 | / | $\frac{1}{4}$ | $\frac{3}{4}$ |
（Ⅰ）求p，q的值；
（Ⅱ）求甲、乙选择不同车型的概率；
（Ⅲ）某市对购买纯电动汽车进行补贴，补贴标准如下表：
| 车型 | A | B | C |
| 补贴金额（万元/辆） | 3 | 4 | 5 |
1．执行如图所示的程序框图，输出的S值为（ ）
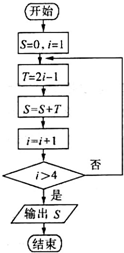
| A． | 9 | B． | 16 | C． | 25 | D． | 36 |