题目内容
设函数f(x)=x+ ,x∈[0,+∞)
,x∈[0,+∞)
(1)当a=2时,求f(x)的最小值.
(2)当0<a<1时,判断f(x)的单调性,并写出f(x)的最小值.
答案:
解析:
解析:
|
解:(1)当a=2时,f(x)=x+ 当且仅当x+1= (2)当0<a<1时,任取x2>x1≥0,则f(x2)-f(x1) =(x2-x1)[1- 因为0<a<1,所以(x1+1)(x2+1)>1,所以 又因为x2>x1,所以x2-x1>0.因此f(x2)-f(x1)>0即f(x)在(0,+∞)上为增函数,所以f(x)的最小值=f(0)=a. |

练习册系列答案
相关题目
 =(x+1)+
=(x+1)+ -1,
-1, -1时取等号,ymin=2
-1时取等号,ymin=2 -1.
-1.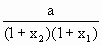 ].
]. <a<1,所以1-
<a<1,所以1-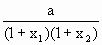 >0.
>0. (k∈R+).
(k∈R+).