题目内容
设函数f(x)=x2-2mx+m2+1(m∈R+),g(x)=x+ (k∈R+).
(k∈R+).
(1)当x∈(0,∞)时,f(x)和g(x)都满足:存在实数a,使f(x)≥f(a),g(x)≥g(a)且f(a)=g(a)-m.求f(x)和g(x)的表达式;
(2)(文科不做、理科做)对于(1)中的f(x),设实数b满足|x-b|<1.
求证:|f(x)-f(b)|<2|b|+5.
答案:
解析:
解析:
|
解: (1)∵当x∈R+时,g(x)=x+ = = + + + + ≥3× ≥3×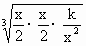 =3 =3 ,当且仅当 ,当且仅当 = = 时,等号成立, 时,等号成立,
即, x=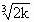 时,g(x)min=3 时,g(x)min=3 , ,
当 x∈R+时,f(x)=(x-m)2+1,∴f(x)min=f(m)=1.∵当 x∈R+时有,f(x)≥f(a),g(x)≥g(a),∴f(a)、g(a)分别是f(x)和g(x)在(0,+∞)上的最小值.∴ 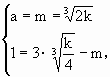 解得,m=2,k=4. 解得,m=2,k=4.
∴ f(x)=x2-4x+5,g(x)=x+ . .
(2)∵|f(x)-f(b)|=|x2-4x-b2+4b|=|(x-b)(x+b)-4)| = |x-b|·|x+b-4|.∵ |x-b|<1, ∴|f(x)-f(b)|<|x+b-4|= |(x-b)+2b-4|≤ |x-b|+|2b|+4< 1+|2b|+4=2|b|+5. |

练习册系列答案
相关题目
 ,x∈[0,+∞)
,x∈[0,+∞)