题目内容
P为双曲线A.b2cot![]() B.
B.![]() absinθ
absinθ
C.|b2-a2|tan![]() D.(a2+b2)sinθ
D.(a2+b2)sinθ
解析:设|PF1|=m,|PF2|=n,由定义知|m-n|=2a,|F1F2|=2c,在△PF1F2内,由余弦定理有
4c2=m2+n2-2mncosθ=(m-n)2+2mn(1-cosθ),
∴mn=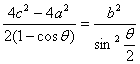 .
.
∴![]() =
=![]() mnsinθ=b2·cot
mnsinθ=b2·cot![]() .
.
答案:A

练习册系列答案
相关题目
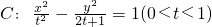 的左右焦点分别为F1,F2,P为双曲线C上任一点,则M=|PF1|+|PF2|-|PF1|•|PF2|的最大值为
的左右焦点分别为F1,F2,P为双曲线C上任一点,则M=|PF1|+|PF2|-|PF1|•|PF2|的最大值为 的左右焦点分别为F1,F2,P为双曲线C上任一点,则M=|PF1|+|PF2|-|PF1|•|PF2|的最大值为( )
的左右焦点分别为F1,F2,P为双曲线C上任一点,则M=|PF1|+|PF2|-|PF1|•|PF2|的最大值为( )