题目内容
已知双曲线 的左右焦点分别为F1,F2,P为双曲线C上任一点,则M=|PF1|+|PF2|-|PF1|•|PF2|的最大值为( )
的左右焦点分别为F1,F2,P为双曲线C上任一点,则M=|PF1|+|PF2|-|PF1|•|PF2|的最大值为( )A.1
B.2
C.1+t2
D.t2+4t+1
【答案】分析:根据双曲线的定义,将函数转化为关于|PF2|的函数,利用配方法,可求其最大值.
解答:解:∵双曲线 ,
,
∴a=t, ,c=t+1
,c=t+1
不妨设|PF1|=2t+|PF2|,|PF2|≥c-a=1
则 ,
,
∴当|PF2|=1时,M有最大值1
故选A.
点评:本题考查双曲线的定义,考查二次函数的最值,解题的关键是将函数转化为关于|PF2|的函数.
解答:解:∵双曲线
 ,
,∴a=t,
 ,c=t+1
,c=t+1不妨设|PF1|=2t+|PF2|,|PF2|≥c-a=1
则
 ,
,∴当|PF2|=1时,M有最大值1
故选A.
点评:本题考查双曲线的定义,考查二次函数的最值,解题的关键是将函数转化为关于|PF2|的函数.

练习册系列答案
 三新快车金牌周周练系列答案
三新快车金牌周周练系列答案
相关题目
 的左右焦点为
的左右焦点为 ,P为双曲线右支上
,P为双曲线右支上 的最小值为8a,则双曲线的离心率的取值范围是 。
的最小值为8a,则双曲线的离心率的取值范围是 。 的左右焦点分别为
的左右焦点分别为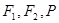 为左支上一点,若
为左支上一点,若 的最小值为
的最小值为 ,则双曲线离心率
,则双曲线离心率 的取值范围为(
)
的取值范围为(
)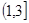 B、
B、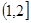 C、
C、 D、
D、
 的左右焦点分别是
的左右焦点分别是 ,
, 点是双曲线右支上一点,且
点是双曲线右支上一点,且 ,则三角形
,则三角形 的面积等于
的面积等于