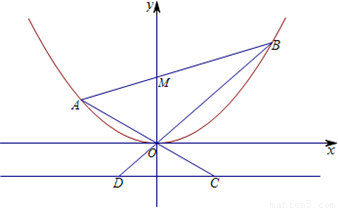
题目内容
已知抛物线E:x2=2py(p>0)的准线方程是y=-
.
(1)求抛物线E的方程;
(2)过点F(0,
)的直线l与抛物线E交于P,Q两点,设N(0,a)(a<0),且
•
≥0恒成立,求实数a的取值范围.
| 1 |
| 2 |
(1)求抛物线E的方程;
(2)过点F(0,
| 1 |
| 2 |
| NP |
| NQ |
分析:(1)由抛物线的准线方程求出p的值,则抛物线的方程可求;
(2)设出直线l的方程,和抛物线方程联立后化为关于x的方程,利用根与系数关系求出两交点的横坐标的和与积,代入
-
≥0后整理得到2k2+1≥a-
,对k∈R恒成立,求出不等式左边的范围后代入不等式求解a的范围.
(2)设出直线l的方程,和抛物线方程联立后化为关于x的方程,利用根与系数关系求出两交点的横坐标的和与积,代入
| NP |
| NQ |
| 3 |
| 4a |
解答:解:(1)∵抛物线的准线方程是y=-
,∴-
=-
,解得p=1,
抛物线E的方程是x2=2y.
(2)设直线l方程是y=kx+
,与x2=2y联立,消去y得,
x2-2kx-1=0,
设P(x1,y1),Q(x2,y2),则x1+x2=2k,x1x2=-1,
∵
•
≥0,∴x1x2+(y1-a)(y2-a)≥0,
又y1y2=
,y1+y2=
=
,
得2k2+1≥a-
,对k∈R恒成立,
而2k2+1≥1,∴a-
≤1(a<0),解得a≤-
.
| 1 |
| 2 |
| p |
| 2 |
| 1 |
| 2 |
抛物线E的方程是x2=2y.
(2)设直线l方程是y=kx+
| 1 |
| 2 |
x2-2kx-1=0,
设P(x1,y1),Q(x2,y2),则x1+x2=2k,x1x2=-1,
∵
| NP |
| NQ |
又y1y2=
| x12x22 |
| 4 |
| x12+x22 |
| 2 |
| (x1+x2)2-2x1x2 |
| 2 |
得2k2+1≥a-
| 3 |
| 4a |
而2k2+1≥1,∴a-
| 3 |
| 4a |
| 1 |
| 2 |
点评:本题考查了抛物线的标准方程,考查了直线与圆锥曲线的关系,考查了数学转化思想方法,训练了一元二次方程的根与系数的关系,训练了分离变量法,属有一定难度题目.

练习册系列答案
 阳光课堂课时优化作业系列答案
阳光课堂课时优化作业系列答案
相关题目
 已知抛物线E的顶点在原点,焦点F在y轴正半轴上,抛物线上一点P(m,4)到其准线的距离为5,过点F的直线l依次与抛物线E及圆x2+(y-1)2=1交于A、C、D、B四点.
已知抛物线E的顶点在原点,焦点F在y轴正半轴上,抛物线上一点P(m,4)到其准线的距离为5,过点F的直线l依次与抛物线E及圆x2+(y-1)2=1交于A、C、D、B四点.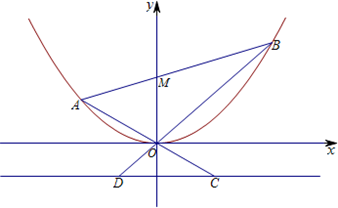 已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.
已知抛物线E:x2=4y,直线l过点M(0,2)且与抛物线交于A、B两点,直线OA、OB分别与抛物线的准线l0交于C、D.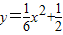 上任意一点,点P在直线l上的射影为Q,求证:PQ=PM;
上任意一点,点P在直线l上的射影为Q,求证:PQ=PM;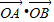 为定值;
为定值;