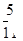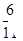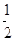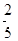题目内容
一个盒子中有5只同型号的灯泡,其中有3只合格品,2只不合格品。现在从中依次取出2只,设每只灯泡被取到的可能性都相同,请用“列举法”解答下列问题:
(1)求第一次取到不合格品,且第二次取到的是合格品的概率;
(2)求至少有一次取到不合格品的概率。
(1)求第一次取到不合格品,且第二次取到的是合格品的概率;
(2)求至少有一次取到不合格品的概率。
(1)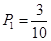 ;(2)
;(2)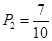
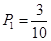 ;(2)
;(2)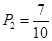
试题分析:令三只合格灯泡分别为a,b,c,两只不合格灯泡分别为e,f,从中取出两只灯泡,所有的取法有ab,ac,ae,af,ba,bc,be,bf,ca,cb,ce,cf,ea,eb,ec,ef,fa,fb,fc,fe总的取法共二十种
(1)第一次取到不合格品,且第二次取到的是合格品取法有6种,分别为ea,eb,ec,fa,fb,fc,故概率是
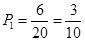 ;
;(2)事件“至少有一次取到不合格品”的对立事件是“取到的全是正品”,“取到的全是正品”包括了六种分别为ab,ac,ba,bc,ca,cb,故事件“至少有一次取到不合格品”取法有14种,至少有一次取到不合格品事件的概率是
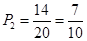
点评:本题主要考查随机事件、互斥事件等概率基础知识,考查运用概率知识解决实际问题的能力

练习册系列答案
相关题目
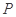 为
为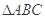 内一点,且
内一点,且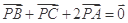 ,在
,在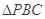 内的概率为( )
内的概率为( )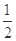
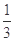
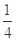
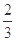
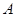 区域返券60元;停在
区域返券60元;停在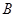 区域返券30元;停在
区域返券30元;停在 区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.
区域不返券. 例如:消费218元,可转动转盘2次,所获得的返券金额是两次金额之和.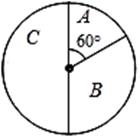
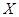 (元),求随机变量
(元),求随机变量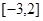 上随机取一个数
上随机取一个数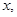 则
则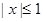 的概率是___________.
的概率是___________.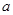 的正方体
的正方体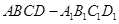 内任取一点
内任取一点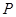 ,则点
,则点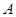 的距离小等于
的距离小等于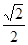
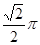
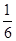
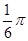
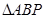 的面积大于
的面积大于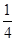 的概率是( )
的概率是( )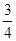
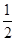
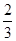
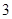 名男生
名男生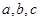 和
和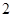 名女生
名女生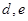 中任选
中任选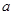 被选中的概率
被选中的概率 至少一人被选中的概率。
至少一人被选中的概率。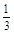
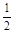
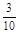
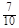
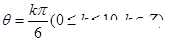 ,则
,则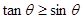 的概率为( )
的概率为( )