Question

下列几个命题
①若方程x²+（a-3）x+a=0有一个正实根，一个负实根，则a＜0．
②函数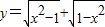是偶函数，但不是奇函数．
③函数f（x）的值域是[-2，2]，则函数f（x+1）的值域为[-3，1]．
④函数y=f（x），x∈R的图象与直线x=a可能有两个不同的交点；
⑤一条曲线y=|3-x²|和直线y=a（a∈R）的公共点个数是m，则m的值不可能是1．
其中正确的有    ．

Answer 1

【答案】分析：①用根的分布来解，令f（x）=x²+（a-3）x+a，一个比0大，一个比0小，只要f（0）＜0即可．可知①正确；②求出函数的定义域，根据定义域确定函数的解析式y=0，故②错；③函数f（x）的值域与函数f（x+1）值域相同，故③错；
④函数表示每个输入值对应唯一输出值的一种对应关系，根据定义进行判定即可判断；⑤画出函数的图象，根据图象可知⑤正确．
解答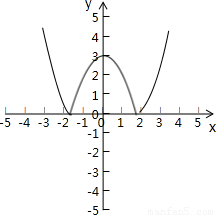：解：①方程x²+（a-3）x+a=0有一个正实根，一个负实根，则a＜0；正确；
②函数的定义域为{-1，1}，∴y=0既是奇函数又是偶函数，故②错；
③函数f（x）的值域与函数f（x+1）值域相同，故③错
④函数表示每个输入值对应唯一输出值的一种对应关系，根据定义进行判定即可判断④错；
⑤根据函数y=|3-x²|的图象可知，⑤正确．
故答案为：①⑤．
点评：此题是个基础题．考查函数图象的对称变化和一元二次方程根的问题，以及函数奇偶性的判定方法等基础知识，考查学生灵活应用知识分析解决问题的能力．