题目内容
下列几个命题:
①关于x的不等式ax<
在(0,1)上恒成立,则a的取值范围为(-∞,1];
②函数y=log2(-x+1)+2的图象可由y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位得到;
③若关于x方程|x2-2x-3|=m有两解,则m=0或m>4;
④若函数f(2x+1)是偶函数,则f(2x)的图象关于直线x=
对称.
其中正确的有
①关于x的不等式ax<
| 2x-x2 |
②函数y=log2(-x+1)+2的图象可由y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位得到;
③若关于x方程|x2-2x-3|=m有两解,则m=0或m>4;
④若函数f(2x+1)是偶函数,则f(2x)的图象关于直线x=
| 1 |
| 2 |
其中正确的有
①②③④
①②③④
.分析:将不等式ax<
化为a<
=
,根据反比例函数及幂函数的性质求出其最小值,可将恒成立问题转化为a的取值范围,进而判断①的真假;
根据函数图象的平移变换法则,可判断平移前后两个函数关系是否符号平移方式,进而得到②的真假;
根据二次函数的图象及函数图象的对折变换法则,分析函数的图象形状及性质,即可分析出方程|x2-2x-3|=m有两解时,m的取值范围,进而判断③的真假;
根据函数图象的平移法则,及偶函数的对称性,可判断③的真假;
| 2x-x2 |
| ||
| x |
|
根据函数图象的平移变换法则,可判断平移前后两个函数关系是否符号平移方式,进而得到②的真假;
根据二次函数的图象及函数图象的对折变换法则,分析函数的图象形状及性质,即可分析出方程|x2-2x-3|=m有两解时,m的取值范围,进而判断③的真假;
根据函数图象的平移法则,及偶函数的对称性,可判断③的真假;
解答:解:关于x的不等式ax<
在(0,1)上恒成立,即a<
=
在(0,1)上恒成立,当x∈(0,1)时,
>1,故a的取值范围为(-∞,1],即①正确;
将y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位可得y=log2[-(x-2]-1)-2+4=log2(-x+1)+2的图象,故②正确;
函数y=|x2-2x-3|是将抛物线y=x2-2x-3的图象位置x轴下方的翻折到x轴上方,且在x=-1或x=3时取极小值0,当x=1时取极大值4,故当m=0或m>4时与直线y=m有两个交点,故③正确;
f(2x)的图象是由f(2x+1)的图象向右平移
个单位得到的,若函数f(2x+1)是偶函数,则其图象关于y轴对称,故f(2x)的图象关于直线x=
对称,即④正确;
故答案为:①②③④
| 2x-x2 |
| ||
| x |
|
|
将y=log2(-x-1)-2的图象向上平移4个单位,向右平移2个单位可得y=log2[-(x-2]-1)-2+4=log2(-x+1)+2的图象,故②正确;
函数y=|x2-2x-3|是将抛物线y=x2-2x-3的图象位置x轴下方的翻折到x轴上方,且在x=-1或x=3时取极小值0,当x=1时取极大值4,故当m=0或m>4时与直线y=m有两个交点,故③正确;
f(2x)的图象是由f(2x+1)的图象向右平移
| 1 |
| 2 |
| 1 |
| 2 |
故答案为:①②③④
点评:本题考查的知识点是命题的真假判断与应用,其中熟练掌握基本初等函数的图象和性质,函数图象的平移变换法则,函数的奇偶性及对称性,是解答的关键.

练习册系列答案
相关题目
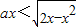 在(0,1)上恒成立,则a的取值范围为(-∞,1];
在(0,1)上恒成立,则a的取值范围为(-∞,1];  对称.
对称. 在(0,1)上恒成立,则a的取值范围为(-∞,1];
在(0,1)上恒成立,则a的取值范围为(-∞,1];  对称.
对称. 在(0,1)上恒成立,则a的取值范围为(-∞,1];
在(0,1)上恒成立,则a的取值范围为(-∞,1];  对称.
对称.