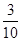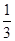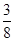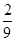袋中装有大小和形状相同的小球若干个黑球和白球.且黑球和白球的个数比为4:3,从中任取2个球都是白球的概率为现不放回从袋中摸取球.每次摸一球.直到取到白球时即终止.每个球在每一次被取出的机会是等可能的.用表示取球终止时所需要的取球次数.(1)求袋中原有白球.黑球的个数,(2)求随机变量的分布列和数学期望. 题目和参考答案——青夏教育精英家教网—

题目内容

袋中装有大小和形状相同的小球若干个黑球和白球，且黑球和白球的个数比为４:３,从中任取2个球都是白球的概率为

现不放回从袋中摸取球，每次摸一球，直到取到白球时即终止，每个球在每一次被取出的机会是等可能的，用

表示取球终止时所需要的取球次数.
（1）求袋中原有白球、黑球的个数；
（2）求随机变量

的分布列和数学期望.

（1）袋中原有3个白球和4个黑球；（2）分布列详见解析，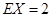

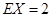试题分析：本题主要考查古典概型、离散型随机变量的分布列和数学期望等基础知识，考查学生的分析问题解决问题的能力、转化能力、计算能力.第一问，设出袋中白球和黑球个数，由于从中任取2个都是白球，则可列出

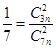，利用组合数的计算，计算出n的值，从而得到白球和黑球个数；第二问，利用第一问的结论，利用不放回抽样，计算出每一种情况的概率，列出分布列，利用

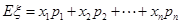计算出数学期望.
（1）依题意设袋中原有

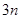个白球,则有

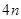个黑球.
由题意知

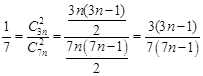， 4分
即

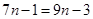，解得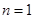

，
即袋中原有3个白球和4个黑球. 5分
（2）依题意，

的取值是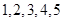

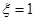，即第1次取到白球，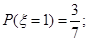

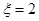，即第2次取到白球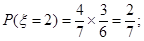

同理可得，

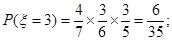
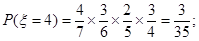
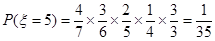10分

分布列为

	1	2	3	4	5

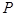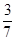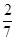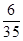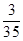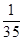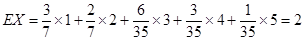12分

练习册系列答案

所用时间（分钟）	10～20	20～30	30～40	40～50	50～60
选择L₁的人数	6	12	18	12	12
选择L₂的人数	0	4	16	16	4

（1）试估计40分钟内不能赶到火车站的概率；
（2）分别求通过路径L₁和L₂所用时间落在上表中各时间段内的频率；
（3）现甲、乙两人分别有40分钟和50分钟时间用于赶往火车站，为了尽量大可能在允许的时间内赶到火车站，试通过计算说明，他们应如何选择各自的路径．

某联欢晚会举行抽奖活动，举办方设置了甲、乙两种抽奖方案，方案甲的中奖率为

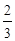，中奖可以获得2分；方案乙的中奖率为

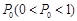，中奖可以获得3分；未中奖则不得分．每人有且只有一次抽奖机会，每次抽奖中奖与否互不影响，晚会结束后凭分数兑换奖品．
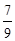（1）张三选择方案甲抽奖，李四选择方案乙抽奖，记他们的累计得分为X，若X≤3的概率为

，求

；
（2）若张三、李四两人都选择方案甲或都选择方案乙进行抽奖，问：他们选择何种方案抽奖，累计得分的数学期望较大？

某篮球决赛在广东队与山东队之间进行，比赛采用7局4胜制，即若有一队先胜4场，则此队获胜，比赛就此结束．因两队实力相当，每场比赛两队获胜的可能性均为

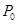．据以往资料统计，第一场比赛组织者可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元，则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________．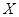

某大学志愿者协会有6名男同学，4名女同学．在这10名同学中，3名同学来自数学学院，其余7名同学来自物理、化学等其他互不相同的七个学院．现从这10名同学中随机选取3名同学，到希望小学进行支教活动（每位同学被选到的可能性相同）．
（1）求选出的3名同学是来自互不相同学院的概率；
（2）设

为选出的3名同学中女同学的人数，求随机变量

的分布列和数学期望．

[2013·北京海淀模拟]已知盒中装有3个红球、2个白球、5个黑球，它们大小形状完全相同，现需一个红球，甲每次从中任取一个不放回，在他第一次拿到白球的条件下，第二次拿到红球的概率(　　)

某学校一位教师要去某地参加全国数学优质课比赛，已知他乘火车、轮船、汽车、飞机直接去的概率分别为0.3、0.1、0.2、0.4.
（1）求他乘火车或乘飞机去的概率；
（2）他不乘轮船去的概率；

若事件A和B是相互独立事件,且P（A·B）＝0.48,P（A·B）＝0.08,P（A）＞P（B）,则P（A）的值为（）
A.0.5 B.0.6 C.0.8 D.0.9

下列随机事件中的随机变量X服从超几何分布的是________．(填序号)
①将一枚硬币连抛3次，正面向上的次数记为X；
②从7男3女共10个学生干部中选出5个优秀学生干部，女生的人数记为X；
③某射手的射击命中率为0.8，现对目标射击1次，记命中的次数为X；
④盒中有4个白球和3个黑球，每次从中摸出1个球且不放回，X是第一次摸出黑球的次数．

试题分类