题目内容
某篮球决赛在广东队与山东队之间进行，比赛采用7局4胜制，即若有一队先胜4场，则此队获胜，比赛就此结束．因两队实力相当，每场比赛两队获胜的可能性均为
．据以往资料统计，第一场比赛组织者可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元，则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________．
．据以往资料统计，第一场比赛组织者可获得门票收入40万元，以后每场比赛门票收入比上一场增加10万元，则组织者在此次决赛中要获得的门票收入不少于390万元的概率为________．
依题意，每场比赛获得的门票收入数组成首项为40，公差为10的等差数列，设此数列为{an}，则易知a1＝40，an＝10n＋30，∴Sn＝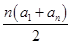
＝
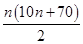．由Sn≥390得n2＋7n≥78，∴n≥6．∴若要获得的门票收入不少于390万元，则至少要比赛6场．①若比赛共进行了6场，则前5场比赛的比分必为2∶3，且第6场比赛为领先一场的球队获胜，其概率P(6)＝
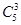×()5＝
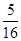；②若比赛共进行了7场，则前6场胜负为3∶3，其概率P(7)＝
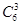×()6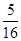＝．∴门票收入不少于390万元的概率P＝P(6)＋P(7)＝
＝．
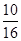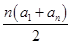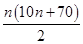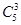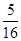＝．由Sn≥390得n2＋7n≥78，∴n≥6．∴若要获得的门票收入不少于390万元，则至少要比赛6场．①若比赛共进行了6场，则前5场比赛的比分必为2∶3，且第6场比赛为领先一场的球队获胜，其概率P(6)＝×()5＝；②若比赛共进行了7场，则前6场胜负为3∶3，其概率P(7)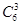＝×()6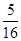＝．∴门票收入不少于390万元的概率P＝P(6)＋P(7)＝＝．
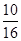练习册系列答案
相关题目
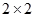列联表：
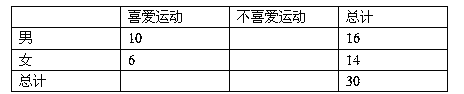
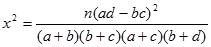（其中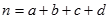
）
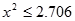
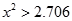
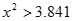
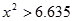
现不放回从袋中摸取球，每次摸一球，直到取到白球时即终止，每个球在每一次被取出的机会是等可能的，用
表示取球终止时所需要的取球次数.
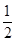成等差数列，
．；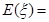