题目内容
[2013·北京海淀模拟]已知盒中装有3个红球、2个白球、5个黑球，它们大小形状完全相同，现需一个红球，甲每次从中任取一个不放回，在他第一次拿到白球的条件下，第二次拿到红球的概率( )
A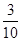． | B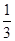． | C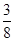． | D． |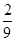
B
事件A：“第一次拿到白球”，B：“第二拿到红球”，则P(A)＝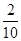
＝
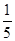，P(AB)＝·
＝
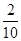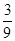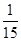，故P(B|A)＝
＝.
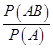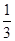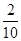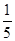＝，P(AB)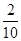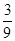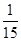＝·＝，故P(B|A)＝＝.
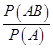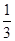练习册系列答案
相关题目
题目内容
| A． | B． | C． | D． |
＝，P(AB)＝·＝，故P(B|A)＝＝.
现不放回从袋中摸取球，每次摸一球，直到取到白球时即终止，每个球在每一次被取出的机会是等可能的，用
表示取球终止时所需要的取球次数.
处刻度不清，根据图表所提供的数据还原
个元件，寿命为
之间的应抽取几个；
个元件，求事件“恰好有一个寿命为
，一个寿命为
”的概率.
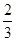,规定有两次回答正确即通过面试,那么该生“通过面试”的概率为 .
，乙获胜的概率为
，则下列说法正确的是( )
