题目内容
1.在直角坐标系中,一动点从点A(1,0)出发,沿单位圆(圆心在坐标原点半径为1的圆)圆周按逆时针方向运动$\frac{2}{3}$π弧长,到达点B,则点B的坐标为( )| A. | (-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$) | B. | (-$\frac{\sqrt{3}}{2}$,-$\frac{1}{2}$) | C. | (-$\frac{1}{2}$,-$\frac{\sqrt{3}}{2}$) | D. | (-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$) |
分析 作出单位圆,过B作BM⊥x轴,交x轴于点M,结合单位圆能求出B点坐标.
解答 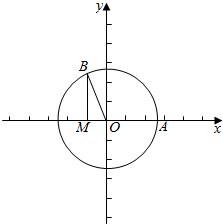 解:如图,作出单位圆,
解:如图,作出单位圆,
由题意,$∠AOB=\frac{2π}{3}$,OB=1,
过B作BM⊥x轴,交x轴于点M,则$∠MOB=\frac{π}{3}$,
∴|OM|=$\frac{1}{2}OB=\frac{1}{2}$,MB=$\sqrt{1-(\frac{1}{2})^{2}}$=$\frac{\sqrt{3}}{2}$,
∴B(-$\frac{1}{2}$,$\frac{\sqrt{3}}{2}$).
故选:A.
点评 本题考查点的坐标的求法,是基础题,解题时要注意单位圆的性质的合理运用.

练习册系列答案
相关题目
11.一炮弹在某处爆炸,在A处听到爆炸声的时间比在B处晚2s,则爆炸点所在曲线为( )
| A. | 椭圆的一部分 | B. | 双曲线的一支 | C. | .线段 | D. | 圆 |
12.奇函数y=f(x)在(-∞,0)上为减函数,且f(2)=0,则不等式f(x)≥0的解集为( )
| A. | (-∞,-2]∪(0,2] | B. | (-∞,-2]∪[2,+∞) | C. | (-∞,-2]∪[0,2] | D. | (-∞,-2]∪{0}∪[2,+∞) |
16.已知集合P={x|x=sin$\frac{(5k-9)π}{3}$,k∈Z},Q={y|y=cos$\frac{5(9-2m)π}{6}$,m∈Z},则P与Q的关系是( )
| A. | P?Q | B. | P?Q | C. | P=Q | D. | P∩Q=∅ |
6.阅读如图所示的程序框图,运行相应的程序,若输出的结果s=16,则图中菱形内应该填写的内容是( )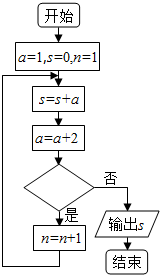

| A. | n<2? | B. | n<3? | C. | n<4? | D. | n<5? |
10.已知a>0,b>0满足a+b=1,则$\frac{1}{a}+\frac{9}{b}$的最小值为( )
| A. | 12 | B. | 16 | C. | 20 | D. | 25 |