题目内容
9．一个几何体的三视图如图所示，则其体积等于$\frac{2}{3}$；表面积等于4+$\sqrt{6}$．
分析 根据几何体的三视图，得出该几何体长方体的一个角，画出图形，结合图形求出它的体积与表面积．
解答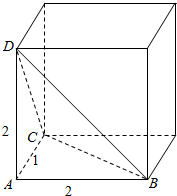 
解：根据几何体的三视图，得；
该几何体是三棱锥，是长宽高分别为2、1、2的长方体的一个角，
如图所示，
则其体积为V=$\frac{1}{3}$×$\frac{1}{2}$×1×2×2=$\frac{2}{3}$；
表面积为S=S△ABD+S△ABC+S△ACD+S△BCD
=$\frac{1}{2}$×2×2+$\frac{1}{2}$×2×1+$\frac{1}{2}$×2×1+$\frac{1}{2}$×2$\sqrt{2}$×$\sqrt{{（\sqrt{5}）}^{2}{-（\sqrt{2}）}^{2}}$
=4+$\sqrt{6}$．
故答案为：$\frac{2}{3}$，4+$\sqrt{6}$．
点评 本题考查了利用三视图求空间几何体的体积与表面积的应用问题，是基础题目．
练习册系列答案
全能练考卷系列答案
相关题目
17．设向量$\overrightarrow a=（cosα，sinα），\overrightarrow b=（cosβ，sinβ）$，其中0＜α＜β＜π，若$|{2\overrightarrow a-\overrightarrow b}|=|{\overrightarrow a+2\overrightarrow b}|$，则β-α=（ ）
| A． | $-\frac{π}{4}$ | B． | $\frac{π}{4}$ | C． | $-\frac{π}{2}$ | D． | $\frac{π}{2}$ |
1．在直角坐标系中，一动点从点A（1，0）出发，沿单位圆（圆心在坐标原点半径为1的圆）圆周按逆时针方向运动$\frac{2}{3}$π弧长，到达点B，则点B的坐标为（ ）
| A． | （-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$） | B． | （-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$） | C． | （-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$） | D． | （-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$） |
18．已知定义域为R的函数f（x）在区间（4，+∞）上为增函数，且函数y=f（x+4）为偶函数，则（ ）
| A． | f（3）＜f（6） | B． | f（3）＜f（5） | C． | f（2）＜f（3） | D． | f（2）＜f（5） |