题目内容

10．已知a＞0，b＞0满足a+b=1，则$\frac{1}{a}+\frac{9}{b}$的最小值为（　　）
A．12B．16C．20D．25

分析 通过“1”的代换，化简所求表达式，利用基本不等式求出它的最小值．

解答 解：∵a＞0，b＞0，且满足a+b=1，
则$\frac{1}{a}+\frac{9}{b}$=$（\frac{1}{a}+\frac{9}{b}）（a+b）$=10+$\frac{b}{a}+\frac{9a}{b}$≥10+2$\sqrt{\frac{b}{a}•\frac{9a}{b}}$=16，
当且仅当$\frac{b}{a}=\frac{9a}{b}$，即a=$\frac{1}{4}$，$b=\frac{1}{2}$时，等号成立．
故$\frac{1}{a}+\frac{9}{b}$的最小值为16，
故选：B．

点评 本题主要考查基本不等式的应用，注意基本不等式的使用条件，并注意检验等号成立的条件，式子的变形是解题的关键，属于基础题．

练习册系列答案
相关题目
20．已知f（x）=2log2（2x+t）
（1）t=1时，解不等式f（x）≤2log2（x+1）
（2）t=4时，令g（x）=f（x）-2log2（x+1），求g（x）在x∈[0，1]上最大值与最小值．
（3）当x∈[0，1]时，f（x）≥log2（x+1）恒成立，求t取值范围？
1．在直角坐标系中，一动点从点A（1，0）出发，沿单位圆（圆心在坐标原点半径为1的圆）圆周按逆时针方向运动$\frac{2}{3}$π弧长，到达点B，则点B的坐标为（　　）
A．（-$\frac{1}{2}$，$\frac{\sqrt{3}}{2}$）B．（-$\frac{\sqrt{3}}{2}$，-$\frac{1}{2}$）C．（-$\frac{1}{2}$，-$\frac{\sqrt{3}}{2}$）D．（-$\frac{\sqrt{3}}{2}$，$\frac{1}{2}$）
18．已知定义域为R的函数f（x）在区间（4，+∞）上为增函数，且函数y=f（x+4）为偶函数，则（　　）
A．f（3）＜f（6）B．f（3）＜f（5）C．f（2）＜f（3）D．f（2）＜f（5）
5．已知函数f（x）=$\frac{x+b}{{1+{x^2}}}$是定义在（-1，1）上的奇函数，
（1）求函数f（x）的解析式；
（2）用单调性的定义证明函数f（x）在（-1，1）上是增函数；
（3）解不等式 f（x2-1）+f（x）＜0．
15．已知等差数列{an}，若a1+a2+a3=-24，a18+a19+a20=78，则S20=180．
2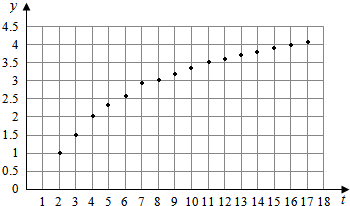．一项实验中获得的一组关于变量y，t之间的数据整理后得到如图所示的散点图．下列函数中可以
近视刻画y与t之间关系的最佳选择是（　　）
A．y=atB．y=logatC．y=at3D．y=a$\sqrt{t}$
19．已知f（x）=|sin$\frac{π}{4006}$x|，x∈[-2003，2003]．
（1）写出满足条件$\frac{1}{2}＜$f（x）＜$\frac{\sqrt{3}}{2}$的两个整数x值（不要求证明）；
（2）若-2003≤x1＜x2＜x3≤2003，且f（x2）＜f（x1）＜f（x3），求证x1x3＜0且x1+x3＞0．
20．已知数列{an}是等差数列，公差d不为零，且a3+a9=a10-a8，则a5=0．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网