题目内容
已知关于x的不等式mx2-2mx+4>0的解集为R,则实数m的取值范围是______.
当m=0时,不等式可化为4>0,显然恒成立
当m≠0时,不等式mx2-2mx+4>0的解集为R
则对应的二次函数y=mx2-2mx+4的图象应开口朝上,且与x轴没有交点
故
,解得0<m<4
综上所述,实数m的取值范围是0≤m<4
故答案为:0≤m<4
当m≠0时,不等式mx2-2mx+4>0的解集为R
则对应的二次函数y=mx2-2mx+4的图象应开口朝上,且与x轴没有交点
故
|
综上所述,实数m的取值范围是0≤m<4
故答案为:0≤m<4

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
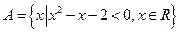 ,
, ,则
,则 =( )
=( )
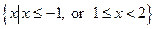


 ,
, ,则
,则 .
.