题目内容
【题目】函数f(x)的定义域为(0,+∞),且对一切x>0,y>0都有![]() ,当
,当![]() 时,有
时,有![]()
(1)求f(1)的值;
(2)判断f(x)的单调性并加以证明;
(3)若f(4)=2,求f(x)在[1,16]上的值域.
【答案】(1)0;(2)见解析;(3)![]() .
.
【解析】试题分析:(1)在恒等式中,令![]() ,即可求得
,即可求得![]() 的值;(2)设
的值;(2)设![]() ,且
,且![]() ,利用恒等式得到
,利用恒等式得到![]() ,根据题中条件,判断
,根据题中条件,判断![]() 的正负,利用函数单调性的定义,即可证明函数的单调性;(3)根据(2)的结论,将值域问题转化为求最值,根据
的正负,利用函数单调性的定义,即可证明函数的单调性;(3)根据(2)的结论,将值域问题转化为求最值,根据![]() ,结合
,结合![]() ,赋值
,赋值![]() ,
, ![]() ,代入即可求得
,代入即可求得![]() ,从而求得
,从而求得![]() 在
在![]() 上的值.
上的值.
试题解析:(1)∵当![]() ,
, ![]() 时,
时, ![]() ,∴令
,∴令![]() ,则
,则![]() .
.
(2)设![]() ,且
,且![]() ,则
,则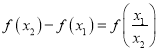 ,∵
,∵![]() ,∴
,∴![]() ,∴
,∴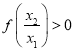 ,∴
,∴![]() ,即
,即![]() 在
在![]() 上是增函数.
上是增函数.
(3)由(2)知![]() 在
在![]() 上是增函数.∴
上是增函数.∴![]() ,
, ![]() ,∵
,∵![]() ,由
,由![]() ,知
,知![]() ,∴
,∴![]() ,∴
,∴![]() 在
在![]() 上的值域为
上的值域为![]() .
.

练习册系列答案
相关题目