题目内容
若抛物线y2=2px的焦点与双曲线 =1的右焦点重合,则p的值为( )
=1的右焦点重合,则p的值为( )
A.-2 B.2 C.-4 D.4
D
【解析】双曲线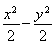 =1的右焦点坐标为(2,0),故
=1的右焦点坐标为(2,0),故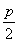 =2,所以p=4.
=2,所以p=4.

练习册系列答案
 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案
相关题目
题目内容
若抛物线y2=2px的焦点与双曲线 =1的右焦点重合,则p的值为( )
=1的右焦点重合,则p的值为( )
A.-2 B.2 C.-4 D.4
D
【解析】双曲线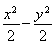 =1的右焦点坐标为(2,0),故
=1的右焦点坐标为(2,0),故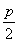 =2,所以p=4.
=2,所以p=4.

 长江作业本同步练习册系列答案
长江作业本同步练习册系列答案