题目内容
16.设函数f(x)=ae2|x-b|(a>0,b∈R),当a=1时,对任意的x∈R,f(x)≥x,求实数b的取值范围.分析 根据解析式得出f(x)的图象关于x=b对称,最小值为f(b)=1,画出f(x)=e2|x-1|与y=x有1个公共点,运用函数图象的平移解决问题.
解答 解:∵a=1,f(x)=e2|x-b|,
∴f(x)的图象关于x=b对称,最小值为f(b)=1,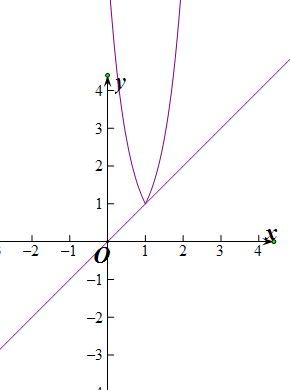
∵任意的x∈R,f(x)≥x,
∴函数f(x)的图象恒在y=x图象的上方,
根据图象可判断,f(x)=e2|x-1|与y=x有1个公共点,
∴当b<1时,f(x)=e2|x-b|,与y=x无公共点,且图象在y=x上方,
故实数b的取值范围为:b≤1,对任意的x∈R,f(x)≥x,
点评 本题考查了指数函数的图象和性质,运用图象的平移,结合函数图象判断字母的取值范围,考查了数形结合的思想,属于中档题.

练习册系列答案
相关题目
4.已知数列{an}满足a1=1,a2=3,an+2=3an(n∈N*)则数列{an}的前2015项的和S2015等于( )
| A. | 31008-2 | B. | 31008-1 | C. | 32015-2 | D. | 32015-3 |
11.称d($\overrightarrow{a},\overrightarrow{b}$)=|$\overrightarrow{a}$-$\overrightarrow{b}$|为两个向量$\overrightarrow{a}$、$\overrightarrow{b}$间的“距离”.若向量$\overrightarrow{a}$、$\overrightarrow{b}$满足:①|$\overrightarrow{b}$|=1;②$\overrightarrow{a}$≠$\overrightarrow{b}$;③对任意的t∈R,恒有d($\overrightarrow{a}$,t$\overrightarrow{b}$)≥d($\overrightarrow{a}$,$\overrightarrow{b}$),则( )
| A. | $\overrightarrow{a}⊥\overrightarrow{b}$ | B. | $\overrightarrow{a}$⊥($\overrightarrow{a}-\overrightarrow{b}$) | C. | $\overrightarrow{b}$⊥($\overrightarrow{a}-\overrightarrow{b}$) | D. | ($\overrightarrow{a}+\overrightarrow{b}$)⊥($\overrightarrow{a}-\overrightarrow{b}$) |
5.在三棱锥P-ABC中,PA,PB,PC两两互相垂直,PA=3,PB=5,PC=$\sqrt{2}$,若三棱锥P-ABC的顶点都在球O的球面上,则球O的体积等于( )
| A. | 36π | B. | 25π | C. | 16π | D. | 4$\sqrt{3}$π |
6.已知集合A={x|y=log2x},B={x∈Z||x|<3},则A∩B=( )
| A. | (0,3) | B. | (-3,+∞) | C. | {1} | D. | {1,2} |