题目内容
(2013•温州二模)己知数列{an}的前n项和为Sn,a1=2.当n≥2时.Sn-1+l,an.Sn+1成等差数列.
(I)求证:{Sn+1}是等比数列:
(II)求数列{nan}的前n项和.
(I)求证:{Sn+1}是等比数列:
(II)求数列{nan}的前n项和.
分析:(I)由题意可得2an=sn+sn-1+2,结合an=sn-sn-1可得sn与sn-1之间的递推关系,进而可证明
(II)由(I)可求sn+1,进而可求sn,然后利用an=sn-sn-1可求an,然后利用错位相减可求Tn
(II)由(I)可求sn+1,进而可求sn,然后利用an=sn-sn-1可求an,然后利用错位相减可求Tn
解答:(I)证明:∵Sn-1+l,an.Sn+1成等差数列
∴2an=sn+sn-1+2…(2分)
∴2(sn-sn-1)=sn+sn-1+2 即sn=3sn-1+2 …(4分)
∴sn+1=3(sn-1+1),n≥2…(6分)
∴{sn+1}是首项为s1+1=3,公比为3的等比数列…(7分)
(II)解:由(I)可知sn+1=3n
∴sn=3n-1…(9分)
当n≥2时,an=sn-sn-1=2•3n-1
又∵a1=3
∴an=2•3n-1…(11分)
∴Tn=2+4•3+6•32+…+2(n-1)•3n-2+2n•3n-1 (1)
3Tn=2•3+4•32+…+(2n-1)•3n-1+2n•3n (2)
(1)-(2)得:
-2Tn=2+2•3+2•32+…+2•3n-1-2n•3n
=
-2n•3n
=3n-1-2n•3n
∴Tn=
…(14分)
∴2an=sn+sn-1+2…(2分)
∴2(sn-sn-1)=sn+sn-1+2 即sn=3sn-1+2 …(4分)
∴sn+1=3(sn-1+1),n≥2…(6分)
∴{sn+1}是首项为s1+1=3,公比为3的等比数列…(7分)
(II)解:由(I)可知sn+1=3n
∴sn=3n-1…(9分)
当n≥2时,an=sn-sn-1=2•3n-1
又∵a1=3
∴an=2•3n-1…(11分)
∴Tn=2+4•3+6•32+…+2(n-1)•3n-2+2n•3n-1 (1)
3Tn=2•3+4•32+…+(2n-1)•3n-1+2n•3n (2)
(1)-(2)得:
-2Tn=2+2•3+2•32+…+2•3n-1-2n•3n
=
| 2(1-3n) |
| 1-3 |
=3n-1-2n•3n
∴Tn=
| (2n-1)•3n+1 |
| 2 |
点评:本题主要考查了利用数列的递推公式构造等比数列求解数列的通项,数列的错位相减求和方法的综合应用

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
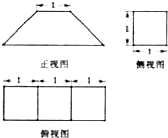 (2013•温州二模)若某几何体的三视图如图所示,则此几何体的体积是( )
(2013•温州二模)若某几何体的三视图如图所示,则此几何体的体积是( )