题目内容
(本小题满分12分)已知函数f (x) = a(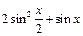 ) + b.
) + b.
(1)当a = 1时,求f (x)的单调递减区间;(2)当a<0时,f (x)在[0,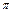 ]上的值域是[2,3],求a,b的值.
]上的值域是[2,3],求a,b的值.
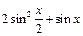 ) + b.
) + b.(1)当a = 1时,求f (x)的单调递减区间;(2)当a<0时,f (x)在[0,
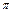 ]上的值域是[2,3],求a,b的值.
]上的值域是[2,3],求a,b的值.(Ⅰ) 递减区间是[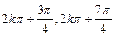 ](k∈Z). (Ⅱ) a = 1–
](k∈Z). (Ⅱ) a = 1–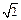 ,b = 3.
,b = 3.
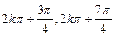 ](k∈Z). (Ⅱ) a = 1–
](k∈Z). (Ⅱ) a = 1–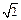 ,b = 3.
,b = 3.(1)当a = 1时,f (x) = 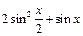 + b =
+ b = 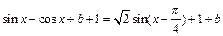
由2k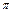 +
+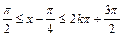 得
得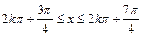 ,
,
∴f (x)的递减区间是[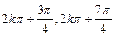 ](k∈Z).……5分
](k∈Z).……5分
(2)f (x) =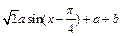 ,∵x∈[0,
,∵x∈[0,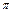 ],∴
],∴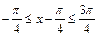 ,∴
,∴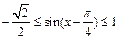
∵a<0,∴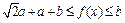 ∵f (x) 的值域是[2,3],∴
∵f (x) 的值域是[2,3],∴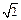 a + a + b = 2且b = 3
a + a + b = 2且b = 3
∴a = 1–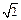 ,b = 3.……10分
,b = 3.……10分
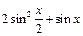 + b =
+ b = 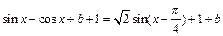
由2k
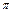 +
+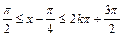 得
得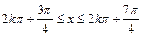 ,
,∴f (x)的递减区间是[
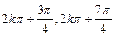 ](k∈Z).……5分
](k∈Z).……5分(2)f (x) =
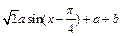 ,∵x∈[0,
,∵x∈[0,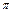 ],∴
],∴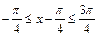 ,∴
,∴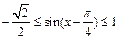
∵a<0,∴
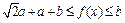 ∵f (x) 的值域是[2,3],∴
∵f (x) 的值域是[2,3],∴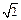 a + a + b = 2且b = 3
a + a + b = 2且b = 3∴a = 1–
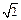 ,b = 3.……10分
,b = 3.……10分
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
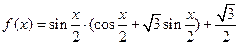 .(1) 求函数
.(1) 求函数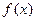 的最小正周期,并写出函数
的最小正周期,并写出函数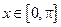 ,求函数
,求函数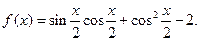
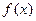 化简成
化简成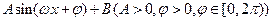 的形式,并指出
的形式,并指出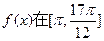 上的最大值和最小值.
上的最大值和最小值.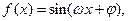 其中
其中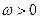 ,
,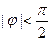 ,
,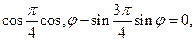 求
求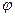 的值;
的值; 

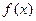 的图象的相邻两条对称轴之间的距离等于
的图象的相邻两条对称轴之间的距离等于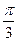 ,求函数
,求函数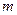 ,使得函数
,使得函数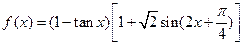 ,求
,求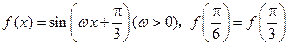 ,且
,且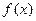 在区间
在区间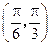 有最小值,无最大值,则
有最小值,无最大值,则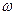 =__________.
=__________. 的定义域为
的定义域为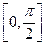 ,值域为
,值域为 .试求函数
.试求函数 (
(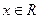 )的最小正周期和最值.
)的最小正周期和最值.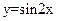 的图象按向量
的图象按向量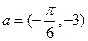 平移后,得到函数
平移后,得到函数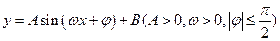 的图象,则
的图象,则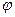 和
和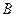 的值依次为
的值依次为


