题目内容
已知 .(1)求函数
.(1)求函数 的值域;(2)求函数
的值域;(2)求函数 的最大值和最小值.
的最大值和最小值.
(1)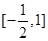 ;(2)最大值:
;(2)最大值: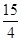 ,最小值
,最小值 .
.
解析试题分析:(1)根据题意 ,由余弦函数的图像易得:当
,由余弦函数的图像易得:当 时,
时, ,当
,当 时,
时, ,即函数
,即函数 的值域
的值域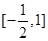 ;
;
(2)将y做如下变形: ,即将y转化为关于cosx的二次函数,设t=cosx, 则
,即将y转化为关于cosx的二次函数,设t=cosx, 则 ,
,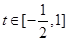 ,二次函数的对称轴为直线t=
,二次函数的对称轴为直线t=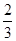 ,根据二次函数求最值的方法,易得y的最大值是
,根据二次函数求最值的方法,易得y的最大值是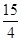 ,最小值是
,最小值是 .
.
(1)∵ ,∴当
,∴当 时,
时, ,当
,当 时,
时, ,∴函数
,∴函数 的值域
的值域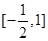 ......4分;
......4分;
(2) ,
,
设t=cosx.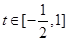 .......6分,
.......6分,
则 ,
,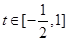 ,二次函数的对称轴为直线
,二次函数的对称轴为直线 ,∵
,∵ ,
,
∴当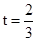 时,y有最小值,
时,y有最小值, ........8分
........8分
当 时,y有最大值
时,y有最大值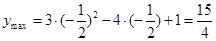 .......10分.
.......10分.
考点:1、三角函数的值域;2、三角函数与二次函数综合.

练习册系列答案
 一诺书业暑假作业快乐假期云南美术出版社系列答案
一诺书业暑假作业快乐假期云南美术出版社系列答案
相关题目
 ).
). 的最小正周期;
的最小正周期; ,求
,求 的值.
的值.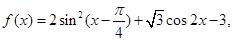
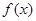 的最小正周期;
的最小正周期;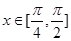 时,求
时,求 ﹣x)满足
﹣x)满足 ,求函数f(x)在
,求函数f(x)在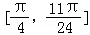 上的最大值和最小值.
上的最大值和最小值. ,
,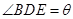 ,
,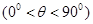 .
.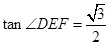 时,求
时,求 的大小;
的大小;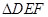 的面积S的最小值及使得S取最小值时
的面积S的最小值及使得S取最小值时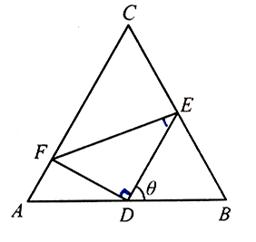
 .
.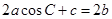 ,求f(B)的取值范围.
,求f(B)的取值范围. sinωxcosωx-cos2ωx,其中ω为使f(x)能在x=
sinωxcosωx-cos2ωx,其中ω为使f(x)能在x= 时取得最大值的最小正整数.
时取得最大值的最小正整数.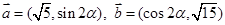 .
.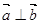 ,且
,且 ,求角
,求角 的值;
的值;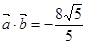 ,且
,且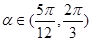 ,求
,求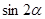 的值.
的值.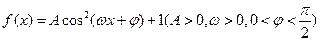 的最大值为3,
的最大值为3, 的图像的相邻两对称轴间的距离为2,在
的图像的相邻两对称轴间的距离为2,在 轴上的截距为2.
轴上的截距为2.