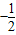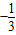题目内容
已知实数a，b满足等式log
a=log
b，下列四个关系式：①0＜b＜a＜1；②0＜a＜b＜1；③1＜b＜a；④a=b，其中不可能成立的关系式有（ ）
| 1 |
| 2 |
| 1 |
| 3 |
分析：先设出对数的值为k，根据对数的定义转化为指数式，根据k的取值范围分为三种情况，由底数的大小判断出a、b的大小关系．
解答：解：设log
a=log
b=k，
∴由对数的定义知，a=(
)k，b=(
)k
故当k＞0时，有0＜b＜a＜1；①可能成立
当k=0时，有a=b；④可能成立
当k＜0时，由1＜a＜b，
②③不可能成立
故选B．
| 1 |
| 2 |
| 1 |
| 3 |
∴由对数的定义知，a=(
| 1 |
| 2 |
| 1 |
| 3 |
故当k＞0时，有0＜b＜a＜1；①可能成立
当k=0时，有a=b；④可能成立
当k＜0时，由1＜a＜b，
②③不可能成立
故选B．
点评：本题考查了对数的定义应用，即把对数式化为指数式，根据底数的对数值得范围进行判断真数的大小．
练习册系列答案
相关题目
已知实数a、b满足条件：ab＜0，且1是a2与b2的等比中项，又是
，
的等差中项，则
的值是（ ）
| 1 |
| a |
| 1 |
| b |
| a+b |
| a2+b2 |
A、
| ||
B、-
| ||
C、
| ||
D、-
|
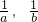的等差中项，则
的值是
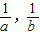的等差中项，则
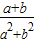的值是（ ）
