题目内容
“α=
”是“cosα=
”的（ ）
| π |
| 3 |
| 1 |
| 2 |
| A、必要不充分条件 |
| B、充分不必要条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
分析：先判断p?q与q?p的真假，再根据充要条件的定义给出结论；也可判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．
解答：解：若“α=
”则“cosα=
”一定成立
若“cosα=
”，则α=2kπ±
，k∈Z，即α=
不一定成立
故“α=
”是“cosα=
”的充分不必要条件
故选B
| π |
| 3 |
| 1 |
| 2 |
若“cosα=
| 1 |
| 2 |
| π |
| 3 |
| π |
| 3 |
故“α=
| π |
| 3 |
| 1 |
| 2 |
故选B
点评：判断充要条件的方法是：①若p?q为真命题且q?p为假命题，则命题p是命题q的充分不必要条件；②若p?q为假命题且q?p为真命题，则命题p是命题q的必要不充分条件；③若p?q为真命题且q?p为真命题，则命题p是命题q的充要条件；④若p?q为假命题且q?p为假命题，则命题p是命题q的即不充分也不必要条件．⑤判断命题p与命题q所表示的范围，再根据“谁大谁必要，谁小谁充分”的原则，判断命题p与命题q的关系．
练习册系列答案
活力课时同步练习册系列答案
学业测评一课一测系列答案
相关题目
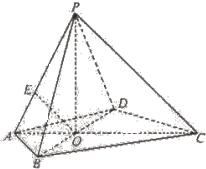如图，在四边形ABCD中，AC⊥BD，垂足为O，PO⊥平面ABCD，AO=BO=DO=1，CO=PO=2，E是线段PA上的点，AE：AP=1：3．
【选修4-1：几何证明选讲】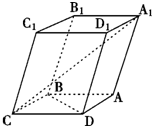
如图，一块矿石晶体的形状为四棱柱，底面ABCD是正方形，CC1=3，CD=2，且∠C1CB=∠C1CD=60°．
已知△OAB是边长为4的正三角形，CO⊥平面OAB，且CO=2，设D、E分别是OA、AB的中点．