题目内容
函数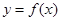 是定义在R上的可导函数,则下列说法不正确的是( )
是定义在R上的可导函数,则下列说法不正确的是( )
A.若函数在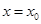 时取得极值,则 时取得极值,则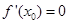 |
B.若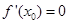 ,则函数在 ,则函数在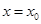 处取得极值 处取得极值 |
C.若在定义域内恒有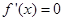 ,则 ,则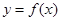 是常数函数 是常数函数 |
D.函数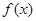 在 在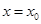 处的导数是一个常数 处的导数是一个常数 |
B.
解析试题分析:对于B,可以构造函数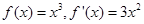 ,则
,则 ,而
,而 并不是
并不是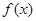 的极值点,而A,C,D均正确,∴选B.
的极值点,而A,C,D均正确,∴选B.
考点:导数的性质.

练习册系列答案
 探究与巩固河南科学技术出版社系列答案
探究与巩固河南科学技术出版社系列答案
相关题目
已知定义域为R的函数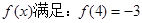 ,且对任意实数x,总有
,且对任意实数x,总有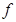 /(x)<3
/(x)<3
则不等式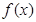 <3x-15的解集为( )
<3x-15的解集为( )
| A.(﹣∞,4) |
| B.(﹣∞,﹣4) |
| C.(﹣∞,﹣4)∪(4,﹢∞) |
| D.(4,﹢∞) |
定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数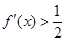 ,则满足
,则满足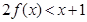 的x的集合为( )
的x的集合为( )
| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |
曲线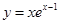 在点(1,1)处切线的斜率等于
在点(1,1)处切线的斜率等于
A.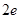 | B. | C.2 | D.1 |
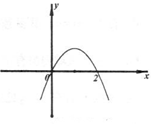
设函数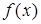 在R上可导,其导函数为
在R上可导,其导函数为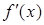 且函数
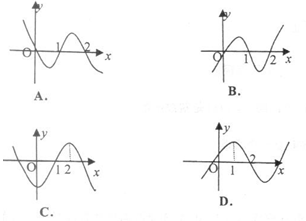
且函数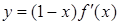 的图像如图所示,则下列结论一定成立的是( )
的图像如图所示,则下列结论一定成立的是( )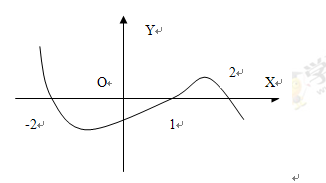
A.函数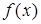 的极大值是 的极大值是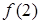 ,极小值是 ,极小值是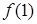 |
B.函数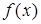 的极大值是 的极大值是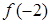 ,极小值是 ,极小值是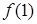 |
C.函数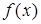 的极大值是 的极大值是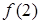 ,极小值是 ,极小值是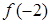 |
D.函数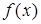 的极大值是 的极大值是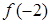 ,极小值是 ,极小值是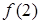 |
定义域为R的函数f(x)满足f(1)=1,且f(x)的导函数 ,则满足
,则满足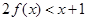 的x的集合为( )
的x的集合为( )
| A.{x|x<1} | B.{x|-1<x<1} | C.{x|x<-1或x>1} | D.{x|x>1} |
直线 在第一象限内围成的封闭图形的面积为( )
在第一象限内围成的封闭图形的面积为( )
A.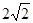 | B.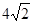 | C.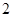 | D.4 |
函数f(x)=x2-2ax+a在区间(-∞,1)上有最小值,则函数g(x)=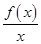 在区间(1,+∞)上一定( )
在区间(1,+∞)上一定( )
| A.有最小值 | B.有最大值 | C.是减函数 | D.是增函数 |
 的导函数
的导函数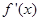 的图像如图所示,则
的图像如图所示,则