题目内容
(2011•浙江)在△ABC中,角A,B,C,所对的边分别为a,b,c.已知sinA+sinC=psinB(p∈R).且ac=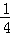 b2.
b2.
(1)当p=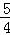 ,b=1时,求a,c的值;
,b=1时,求a,c的值;
(2)若角B为锐角,求p的取值范围.
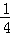 b2.
b2.(1)当p=
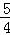 ,b=1时,求a,c的值;
,b=1时,求a,c的值;(2)若角B为锐角,求p的取值范围.
(1)a=1,c= 或a=
或a= ,c=1 (2)
,c=1 (2) <p<
<p<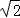
 或a=
或a= ,c=1 (2)
,c=1 (2) <p<
<p<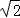
(1)解:由题设并利用正弦定理得
故可知a,c为方程x2﹣ x+
x+ =0的两根,
=0的两根,
进而求得a=1,c= 或a=
或a= ,c=1
,c=1
(2)解:由余弦定理得b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣2accosB=p2b2﹣ b2cosB﹣
b2cosB﹣ ,
,
即p2=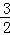 +
+ cosB,
cosB,
因为0<cosB<1,
所以p2∈(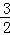 ,2),由题设知p∈R,所以
,2),由题设知p∈R,所以 <p<
<p<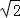 或﹣
或﹣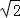 <p<﹣
<p<﹣
又由sinA+sinC=psinB知,p是正数
故 <p<
<p<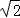 即为所求
即为所求

故可知a,c为方程x2﹣
 x+
x+ =0的两根,
=0的两根,进而求得a=1,c=
 或a=
或a= ,c=1
,c=1(2)解:由余弦定理得b2=a2+c2﹣2accosB=(a+c)2﹣2ac﹣2accosB=p2b2﹣
 b2cosB﹣
b2cosB﹣ ,
,即p2=
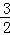 +
+ cosB,
cosB,因为0<cosB<1,
所以p2∈(
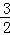 ,2),由题设知p∈R,所以
,2),由题设知p∈R,所以 <p<
<p<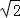 或﹣
或﹣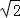 <p<﹣
<p<﹣
又由sinA+sinC=psinB知,p是正数
故
 <p<
<p<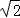 即为所求
即为所求
练习册系列答案
相关题目
 中,已知
中,已知 ,解三角形
,解三角形 .
.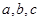 是
是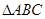 的三条边的长,对任意实数
的三条边的长,对任意实数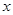 ,
,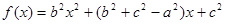 有 ( )
有 ( )



 ,b=5,求sinBsinC的值.
,b=5,求sinBsinC的值. ,测得塔基的俯角为
,测得塔基的俯角为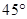 ,那么塔的高度是( )米.
,那么塔的高度是( )米.



 ,在
,在 上取一点P,使
上取一点P,使 ,求
,求
