题目内容
某人站在60米高的楼顶A处测量不可到达的电视塔的高度,测得塔顶C的仰角为30°,塔底B的俯角为15°,已知楼底部D和电视塔的底部B在同一水平面上,则电视塔的高为 米.
120+40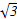
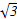
如图,用AD表示楼高,AE与水平面平行,E在线段BC上,
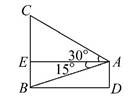
因为∠CAE=30°,∠BAE=15°,AD=BE=60,
则AE=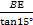 =
=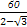 =120+60
=120+60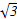 ,
,
在Rt△AEC中,
CE=AE·tan30°=(120+60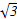 )×
)×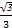 =60+40
=60+40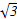 ,
,
∴BC=CE+BE=60+40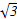 +60=(120+40
+60=(120+40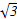 )米,
)米,
所以塔高为(120+40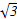 )米.
)米.

因为∠CAE=30°,∠BAE=15°,AD=BE=60,
则AE=
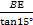 =
=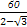 =120+60
=120+60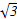 ,
,在Rt△AEC中,
CE=AE·tan30°=(120+60
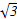 )×
)×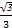 =60+40
=60+40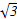 ,
,∴BC=CE+BE=60+40
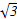 +60=(120+40
+60=(120+40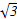 )米,
)米,所以塔高为(120+40
 )米.
)米.
练习册系列答案
相关题目
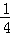 b2.
b2.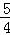 ,b=1时,求a,c的值;
,b=1时,求a,c的值;
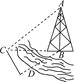
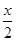 -
-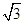 sin x.
sin x.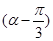 =
=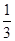 ,求
,求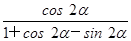 的值.
的值.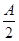 sin
sin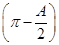 +sin2
+sin2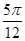 ,a=
,a=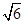 ,求b的值.
,求b的值.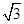 ,则AB+2BC的最大值为________.
,则AB+2BC的最大值为________.