题目内容
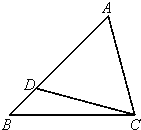
在△ABC中，D为BC边上一点，BC=3BD，AD=| 2 |
| 2 |
分析：先利用余弦定理可分别表示出AB，AC，把已知条件代入整理，根据BC=3BD推断出CD=2BD，进而整理 AC2=CD2+2-2CD 得AC2=4BD2+2-4BD把AC=
AB，代入整理，最后联立方程消去AB求得BD的方程求得BD．
| 2 |
解答：用余弦定理求得
AB2=BD2+AD2-2AD•BDcos135°
AC2=CD2+AD2-2AD•CDcos45°
即 AB2=BD2+2+2BD ①AC2=CD2+2-2CD ②
又BC=3BD
所以 CD=2BD
所以 由（2）得AC2=4BD2+2-4BD（3）
因为 AC=
AB
所以 由（3）得 2AB2=4BD2+2-4BD （4）
（4）-2（1）
BD2-4BD-1=0
求得 BD=2+
故答案为：2+
AB2=BD2+AD2-2AD•BDcos135°
AC2=CD2+AD2-2AD•CDcos45°
即 AB2=BD2+2+2BD ①AC2=CD2+2-2CD ②
又BC=3BD
所以 CD=2BD
所以 由（2）得AC2=4BD2+2-4BD（3）
因为 AC=
| 2 |
所以 由（3）得 2AB2=4BD2+2-4BD （4）
（4）-2（1）
BD2-4BD-1=0
求得 BD=2+
| 5 |
故答案为：2+
| 5 |
点评：本题主要考查了余弦定理的应用．考查了学生创造性思维能力和基本的推理能力．
练习册系列答案
名校课堂系列答案
相关题目
在△ABC中，D为BC的中点，已知
=
，
=
，则下列向量一定与
同向的是（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
如图，在△ABC中，D为边AB上一点，DA=DC．已知B=