题目内容
在△ABC中，D为BC中点，a，b，c成等差数列且a+c=8，cosB=
，a＞c，则
•
等于（ ）
| 3 |
| 5 |
| AD |
| BC |
分析：由已知，先求出b=4，利用余弦定理由cosB=
得出a、c关系式，解出a，c，而
•
=
(
+
)(
-
求解计算．
| 3 |
| 5 |
| AD |
| BC |
| 1 |
| 2 |
| AB |
| AC |
| AC |
| AB) |
解答：解：∵a，b，c成等差数列，a+c=8，
∴2b=8，b=4．
cosB=
=
=
=
，得出ac=15，与a+c=8联立解得a=5，c=3．
∴
•
=
(
+
)(
-
=
（
2-
2）=
（b2-c2）=
故选C．
∴2b=8，b=4．
cosB=
| 3 |
| 5 |
| a2+c2-b2 |
| 2ac |
| (a+c)2 -2ac-b2 |
| 2ac |
| 48 -2ac |
| 2ac |
∴
| AD |
| BC |
| 1 |
| 2 |
| AB |
| AC |
| AC |
| AB) |
| 1 |
| 2 |
| AC |
| AB |
| 1 |
| 2 |
| 7 |
| 2 |
故选C．
点评：本题考查余弦定理的应用，向量加法的几何意义，向量数量积的运算．
练习册系列答案
相关题目
在△ABC中，D为BC的中点，已知
=
，
=
，则下列向量一定与
同向的是（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
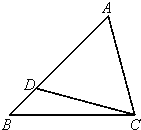如图，在△ABC中，D为边AB上一点，DA=DC．已知B=