题目内容
在△ABC中，D为BC边中点，∠B+∠DAC=90°，判断△ABC的形状．
分析：由条件求得∠DAC=90°-∠B，∠DAB=90°-∠C．△ABD中利用正弦定理，△ADC中，利用正弦定理，化简可得
sin2B=sin2C，可得2B=2C，或2B+2C=π，从而得到△ABC为等腰或直角三角形．
sin2B=sin2C，可得2B=2C，或2B+2C=π，从而得到△ABC为等腰或直角三角形．
解答：解：
，
∴
，∴∠DAC=90°-∠B，∠DAB=90°-∠C． …（2分）
在△ABD中，
=
，在△ADC中，
=
．…（6分）
两式相比得sinCcosC=sinBcosB，…（8分）
即sin2B=sin2C，
∴2B=2C，或2B+2C=π，故△ABC为等腰或直角三角形．…（12分）
|
∴
|
在△ABD中，
| AD |
| sinB |
| BD |
| sin(90°-∠C) |
| AD |
| sinC |
| DC |
| sin(90°-∠B) |
两式相比得sinCcosC=sinBcosB，…（8分）
即sin2B=sin2C，
∴2B=2C，或2B+2C=π，故△ABC为等腰或直角三角形．…（12分）
点评：本题主要考查正弦定理的应用，三角形的内角和公式、以及二倍角公式的应用，属于中档题．
练习册系列答案
相关题目
在△ABC中，D为BC的中点，已知
=
，
=
，则下列向量一定与
同向的是（ ）
| AB |
| a |
| AC |
| b |
| AD |
A、
| ||||||||||||
B、
| ||||||||||||
C、
| ||||||||||||
D、
|
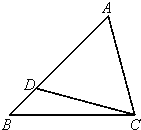如图，在△ABC中，D为边AB上一点，DA=DC．已知B=