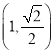题目内容
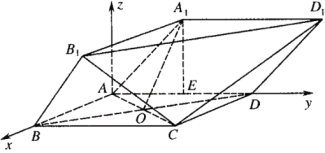
【题目】由四棱柱![]() 截去三棱锥
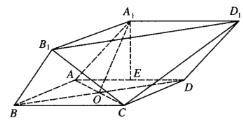
截去三棱锥![]() 后得到的几何体如图所示,四边形
后得到的几何体如图所示,四边形![]() 是边长为
是边长为![]() 的正方形,
的正方形,![]() 为
为![]() 与
与![]() 的交点,
的交点,![]() 为
为![]() 的中点,
的中点,![]() 平面
平面![]() .
.
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,求线段
,求线段![]() 的长.
的长.
【答案】(Ⅰ)证明见解析;(Ⅱ)![]() .
.
【解析】
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,证明四边形
,证明四边形![]() 为平行四边形,可得出
为平行四边形,可得出![]() ,再利用线面平行的判定定理可证明出
,再利用线面平行的判定定理可证明出![]() 平面
平面![]() ;
;
(Ⅱ)以点![]() 为坐标原点,
为坐标原点,![]() 、
、![]() 所在直线分别为
所在直线分别为![]() 、
、![]() 轴建立空间直角坐标系,设
轴建立空间直角坐标系,设![]() ,计算出平面
,计算出平面![]() 的一个法向量,利用直线
的一个法向量,利用直线![]() 与平面
与平面![]() 所成的角为
所成的角为![]() ,计算出
,计算出![]() 的值,进而得解.
的值,进而得解.
(Ⅰ)取![]() 的中点
的中点![]() ,连接
,连接![]() 、
、![]() ,
,
由于![]() 为四棱柱,所以,
为四棱柱,所以,![]() 且
且![]() ,
,
![]() 四边形
四边形![]() 为平行四边形,则
为平行四边形,则![]() 且
且![]() ,
,
![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点,所以
的中点,所以![]() ,且
,且![]() ,
,
因此四边形![]() 为平行四边形,所以
为平行四边形,所以![]() .
.
又![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,所以
,所以![]() 平面
平面![]() ;
;
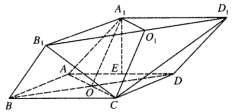
(Ⅱ)如图,建立空间直角坐标系,设![]() ,
,
易知![]() 、
、![]() 、
、![]() 、
、![]() ,从而可得
,从而可得![]() .
.
设平面![]() 的法向量为
的法向量为![]() ,
,
又![]() ,
,![]() ,故有
,故有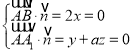 ,解得
,解得![]() ,
,
可取![]() .
.
由题意得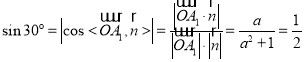 ,
,
解得![]() ,即线段
,即线段![]() 的长为
的长为![]() .
.

 直通贵州名校周测月考直通名校系列答案
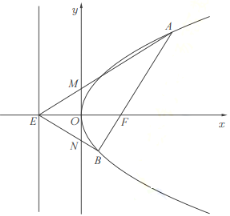
直通贵州名校周测月考直通名校系列答案【题目】如图,在平面直角坐标系![]() 中,已知抛物线
中,已知抛物线![]() 的焦点为
的焦点为![]() ,准线与
,准线与![]() 轴的交点为
轴的交点为![]() .过点
.过点![]() 的直线与抛物线相交于
的直线与抛物线相交于![]() 、
、![]() 两点,
两点,![]() 、
、![]() 分别与
分别与![]() 轴相交于
轴相交于![]() 、
、![]() 两点,当
两点,当![]() 轴时,
轴时,![]() .
.
(1)求抛物线的方程;
(2)设![]() 的面积为
的面积为![]() ,
,![]() 面积为
面积为![]() ,求
,求![]() 的取值范围.
的取值范围.
【题目】某健身机构统计了去年该机构所有消费者的消费金额(单位:元),如下图所示:

(1)将去年的消费金额超过 3200 元的消费者称为“健身达人”,现从所有“健身达人”中随机抽取 2 人,求至少有 1 位消费者,其去年的消费金额超过 4000 元的概率;
(2)针对这些消费者,该健身机构今年欲实施入会制,详情如下表:
会员等级 | 消费金额 |
普通会员 | 2000 |
银卡会员 | 2700 |
金卡会员 | 3200 |
预计去年消费金额在![]() 内的消费者今年都将会申请办理普通会员,消费金额在
内的消费者今年都将会申请办理普通会员,消费金额在![]() 内的消费者都将会申请办理银卡会员,消费金额在
内的消费者都将会申请办理银卡会员,消费金额在![]() 内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
内的消费者都将会申请办理金卡会员. 消费者在申请办理会员时,需-次性缴清相应等级的消费金额.该健身机构在今年底将针对这些消费者举办消费返利活动,现有如下两种预设方案:
方案 1:按分层抽样从普通会员, 银卡会员, 金卡会员中总共抽取 25 位“幸运之星”给予奖励: 普通会员中的“幸运之星”每人奖励 500 元; 银卡会员中的“幸运之星”每人奖励 600 元; 金卡会员中的“幸运之星”每人奖励 800 元.
方案 2:每位会员均可参加摸奖游戏,游戏规则如下:从-个装有 3 个白球、 2 个红球(球只有颜色不同)的箱子中, 有放回地摸三次球,每次只能摸-个球.若摸到红球的总数消费金额/元为 2,则可获得 200 元奖励金; 若摸到红球的总数为 3,则可获得 300 元奖励金;其他情况不给予奖励. 规定每位普通会员均可参加 1 次摸奖游戏;每位银卡会员均可参加 2 次摸奖游戏;每位金卡会员均可参加 3 次摸奖游戏(每次摸奖的结果相互独立) .
以方案 2 的奖励金的数学期望为依据,请你预测哪-种方案投资较少?并说明理由.
【题目】为抗击新型冠状病毒,普及防护知识,某校开展了“疫情防护”网络知识竞赛活动.现从参加该活动的学生中随机抽取了100名学生,将他们的比赛成绩(满分为100分)分为6组:![]() ,得到如图所示的频率分布直方图.
,得到如图所示的频率分布直方图.
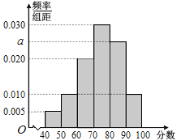
(1)求![]() 的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
的值,并估计这100名学生的平均成绩(同一组中的数据用该组区间的中点值为代表);
(2)在抽取的100名学生中,规定:比赛成绩不低于80分为“优秀”,比赛成绩低于80分为“非优秀”.请将下面的2×2列联表补充完整,并判断是否有99%的把握认为“比赛成绩是否优秀与性别有关”?
优秀 | 非优秀 | 合计 | |
男生 | 40 | ||
女生 | 50 | ||
合计 | 100 |
参考公式及数据:![]() .
.
| 0.05 | 0.01 | 0.005 | 0.001 |
| 3.841 | 6.635 | 7.879 | 10.828 |