题目内容
如图,四棱锥P-ABCD的底面是菱形,∠ABC=60°,PA⊥底面ABCD,E、F分别是BC、PC的中点,PA=AB=2.(1)求证:AE⊥PD;
(2)求三棱锥A-EFC的体积.

【答案】分析:(1)依题意,在△ABE中,由AB=2,BE=1,∠ABC=60°,可证得AE⊥BC,从而得AE⊥AD,于是由线面垂直的判断定理可证得AE⊥平面PAD,继而可得AE⊥PD;
(2)可取AC的中点O,连接FO,由VA-EFC=VF-AEC即可求得答案.
解答:证明:(1)依题意,在等腰△ABC中,∠ABC=60°,
∴△ABC为等边三角形,又E是BC的中点,
∴AE⊥BC,又BC∥AD,
∴AE⊥AD;
∵PA⊥底面ABCD,AE?底面ABCD,
∴AE⊥PA;
PA∩AD=A,
∴AE⊥平面PAD,PD?平面PAD,
∴AE⊥PD;
(2)连接BD与AC相交于O,连接FO,则O为AC的中点,又F是PC的中点,
∴FO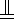
 PA=1,由PA⊥底面ABCD知,FO⊥底面ABCD;
PA=1,由PA⊥底面ABCD知,FO⊥底面ABCD;
又AE=2sin60°=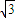 ,EC=1,
,EC=1,
∴VA-EFC=VF-AEC
= ×
× ×AE×EC×FO
×AE×EC×FO
= ×
×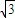 ×1×1
×1×1
=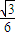 .
.
点评:本题考查直线与平面垂直判断与性质,考查棱锥的体积,考查推理与运算能力,属于中档题.
(2)可取AC的中点O,连接FO,由VA-EFC=VF-AEC即可求得答案.
解答:证明:(1)依题意,在等腰△ABC中,∠ABC=60°,
∴△ABC为等边三角形,又E是BC的中点,
∴AE⊥BC,又BC∥AD,
∴AE⊥AD;
∵PA⊥底面ABCD,AE?底面ABCD,
∴AE⊥PA;
PA∩AD=A,
∴AE⊥平面PAD,PD?平面PAD,
∴AE⊥PD;
(2)连接BD与AC相交于O,连接FO,则O为AC的中点,又F是PC的中点,
∴FO
 PA=1,由PA⊥底面ABCD知,FO⊥底面ABCD;
PA=1,由PA⊥底面ABCD知,FO⊥底面ABCD;又AE=2sin60°=
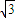 ,EC=1,
,EC=1,∴VA-EFC=VF-AEC
=
 ×
× ×AE×EC×FO
×AE×EC×FO=
 ×
×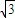 ×1×1
×1×1=
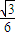 .
.点评:本题考查直线与平面垂直判断与性质,考查棱锥的体积,考查推理与运算能力,属于中档题.

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目
 如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC,
如图,四棱锥P-ABCD中,PA⊥底面ABCD,AB⊥AD,AC⊥CD,∠ABC=60°,PA=AB=BC, 如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点.
如图,四棱锥P-ABCD中,底面ABCD是直角梯形,AB∥CD,∠DAB=60°,AB=AD=2CD=2,侧面PAD⊥底面ABCD,且△PAD为等腰直角三角形,∠APD=90°,M为AP的中点. 如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2,
如图,四棱锥P-ABCD的底面ABCD是矩形,AB=2, 如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1,
如图,四棱锥P-ABCD中,底面ABCD为矩形,PA⊥底面ABCD,且PA=AB=1, 如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=
如图,四棱锥P-ABCD,PA⊥平面ABCD,ABCD是直角梯形,DA⊥AB,CB⊥AB,PA=2AD=BC=2,AB=