题目内容
同时抛掷两枚大小形状都相同、质地均匀的骰子,求:
(1)一共有多少种不同的结果;
(2)点数之和4的概率;
(3)至少有一个点数为5的概率.
(1)一共有多少种不同的结果;
(2)点数之和4的概率;
(3)至少有一个点数为5的概率.
(1)36(2)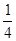 (3)
(3)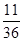
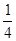 (3)
(3)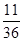
试题分析:(1)每一个一个正方体骰子的结果有6种,因此同时抛掷两枚质地均匀的正方体骰子的结果有36种.
(2)用列举法求得在上面所有结果中其中点数之和是4的倍数的有9种,所以P(A)
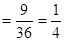 .
.(3)由于所有36种结果是等可能的,其中至少有一个点数为5的结果有(1,5)(2,5)(3,5)
(4,5)(5,5)(6,5)(5,1)(5,2)(5,3)(5,4)(5,6)共11个,从而求得概率.古典概型问题,可以列举出试验发生包含的事件和满足条件的事件,列举法,是解决古典概型问题的一种重要的解题方法.
试题解析:(1)掷一枚骰子的结果有6种 1分 我们把两个骰子标上记1,2以便区分,由于1号
骰子的每一个结果都可以与2号骰子的任意一个结果配对,组成同时掷两枚骰子的一个结果 3分
因此同时掷两枚骰子的结果共有36种。 4分
(2)记事件A为“点数之和是4的倍数”,则A包含的基本事件为:(1,3)(2,2)(2,6)
(3,1)(3,5)(4,4)(5,3)(6,2)(6,6)共9个。 7分
所以P(A)
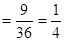 9分
9分(3)记事件B为“至少有一个点数为5”,则事件B包含的基本事件为:(1,5)(2,5)(3,5)
(4,5)(5,5)(6,5)(5,1)(5,2)(5,3)(5,4)(5,6)共11个。 12分
所以P(B)
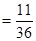 14分
14分
练习册系列答案
相关题目
 小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
小时抽一包产品,称其重量(单位:克)是否合格,分别记录抽查数据,获得重量数据的茎叶图如图所示.
 件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过
件样品中随机抽取两件,求所抽取的两件样品的重量之差不超过 克的概率.
克的概率.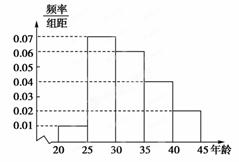
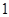 ,
,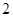 ,
,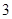 ,
,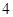 ,
,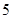 五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下:
五个等级.现从一批该产品随机抽取20个,对其等级进行统计分析,得到频率分布表如下: 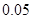
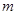
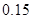
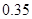
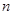
 和p.
和p. ,求p的值;
,求p的值; ,对于
,对于 ,记
,记 ,且
,且 ,由所有
,由所有 组成的集合记为:
组成的集合记为: ,
, 的值为________;
的值为________; ,对任意
,对任意 ,
, ,则
,则 的概率为________.
的概率为________.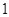 小时收费
小时收费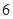 元,超过
元,超过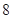 元(不足
元(不足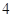 小时.
小时.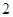 小时的概率为
小时的概率为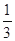 ,停车付费多于
,停车付费多于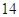 元的概率为
元的概率为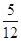 ,求甲停车付费恰为
,求甲停车付费恰为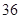 元的概率.
元的概率.