题目内容
某居民小区有两个相互独立的安全防范系统(简称系统)A和B,系统A和B在任意时刻发生故障的概率分别为 和p.
和p.
(1)若在任意时刻至少有一个系统不发生故障的概率为 ,求p的值;
,求p的值;
(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
 和p.
和p.(1)若在任意时刻至少有一个系统不发生故障的概率为
 ,求p的值;
,求p的值;(2)设系统A在3次相互独立的检测中不发生故障的次数为随机变量ξ,求ξ的概率分布列及数学期望Eξ.
(1)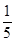 (2)
(2)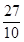
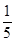 (2)
(2)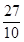
(1)设“至少有一个系统不发生故障”为事件C,那么
1-P(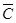 )=1-
)=1- ·p=
·p= .
.
解得p=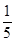 .
.
(2)由题意,P(ξ=0)=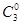
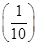 3=
3=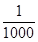 ,
,
P(ξ=1)=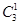
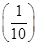 2·
2·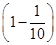 =
=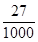 ,
,
P(ξ=2)=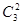
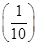 ·
·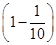 2=
2=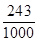 ,
,
P(ξ=3)=
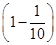 3=
3=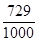 .
.
所以,随机变量ξ的概率分布列为
故随机变量ξ的数学期望:
E(ξ)=0×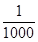 +1×
+1×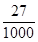 +2×
+2×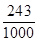 +3×
+3×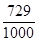 =
=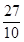
1-P(
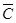 )=1-
)=1- ·p=
·p= .
.解得p=
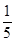 .
.(2)由题意,P(ξ=0)=
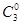
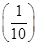 3=
3=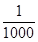 ,
,P(ξ=1)=
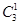
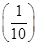 2·
2·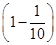 =
=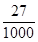 ,
,P(ξ=2)=
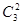
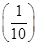 ·
·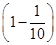 2=
2=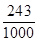 ,
,P(ξ=3)=

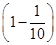 3=
3=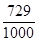 .
.所以,随机变量ξ的概率分布列为
| ξ | 0 | 1 | 2 | 3 |
| P | 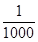 | 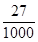 | 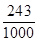 | 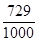 |
E(ξ)=0×
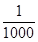 +1×
+1×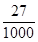 +2×
+2×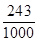 +3×
+3×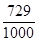 =
=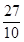

练习册系列答案
 全优冲刺100分系列答案
全优冲刺100分系列答案 英才点津系列答案
英才点津系列答案
相关题目
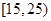
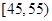

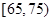
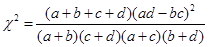 ,
,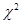 <2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
<2.706时,没有充分的证据判定赞不赞成楼市限购令与收入高低有关;
