题目内容
已知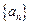 是公差为
是公差为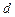 的等差数列,它的前
的等差数列,它的前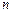 项和为
项和为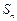 , 等比数列
, 等比数列 的前
的前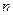 项和为
项和为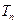 ,
,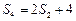 ,
,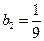 ,
,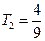
(1)求公差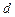 的值;
的值;
(2)若对任意的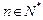 ,都有
,都有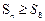 成立,求
成立,求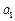 的取值范围;
的取值范围;
(3)若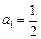 ,判别方程
,判别方程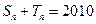 是否有解?说明理由.
是否有解?说明理由.
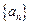 是公差为
是公差为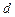 的等差数列,它的前
的等差数列,它的前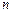 项和为
项和为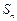 , 等比数列
, 等比数列 的前
的前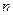 项和为
项和为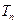 ,
,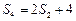 ,
,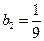 ,
,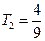
(1)求公差
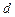 的值;
的值;(2)若对任意的
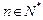 ,都有
,都有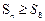 成立,求
成立,求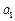 的取值范围;
的取值范围;(3)若
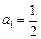 ,判别方程
,判别方程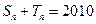 是否有解?说明理由.
是否有解?说明理由.解:(1)∵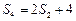 ,∴
,∴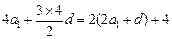 …………(4分)
…………(4分)
解得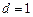 …………(6分)
…………(6分)
(2)由于等差数列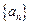 的公差
的公差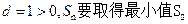
必须有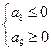
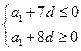 ………(10分)
………(10分)
求得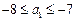 ∴
∴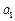 的取值范围是
的取值范围是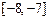 ………(12分)
………(12分)
(3)由于等比数列 满足
满足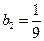 ,
,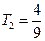

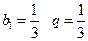

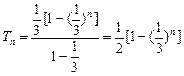 ,
,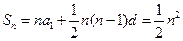 ……(14分)
……(14分)
则方程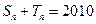 转化为:
转化为: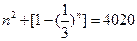
令: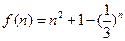 ,知
,知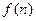 单调递增 ……(16分)
单调递增 ……(16分)
当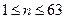 时,
时,
当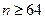 时,
时,
所以 方程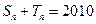 无解.
无解.
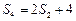 ,∴
,∴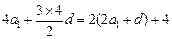 …………(4分)
…………(4分)解得
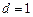 …………(6分)
…………(6分)(2)由于等差数列
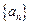 的公差
的公差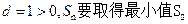
必须有
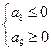
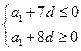 ………(10分)
………(10分)求得
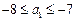 ∴
∴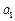 的取值范围是
的取值范围是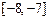 ………(12分)
………(12分)(3)由于等比数列
 满足
满足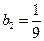 ,
,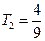

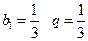

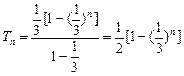 ,
,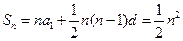 ……(14分)
……(14分)则方程
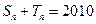 转化为:
转化为: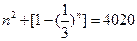
令:
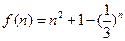 ,知
,知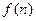 单调递增 ……(16分)
单调递增 ……(16分)当
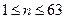 时,
时,
当
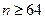 时,
时,
所以 方程
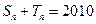 无解.
无解.略

练习册系列答案
 备战中考寒假系列答案
备战中考寒假系列答案
相关题目
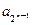 ,…,构成一个新的数列{bn},求{bn}的前n项和.
,…,构成一个新的数列{bn},求{bn}的前n项和.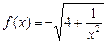 ,点
,点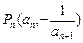 在曲线
在曲线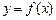 上
上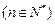 且
且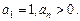 (Ⅰ)求证:数列
(Ⅰ)求证:数列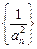 为等差数列,并求数列
为等差数列,并求数列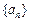 的通项公式;
的通项公式;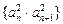 的前n项和为
的前n项和为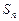 ,若对于任意的
,若对于任意的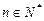 ,存在正整数t,使得
,存在正整数t,使得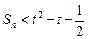 恒成立,求最小正整数t的值.
恒成立,求最小正整数t的值.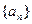 的各项均为正数,
的各项均为正数,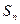 是数列
是数列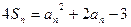 .
.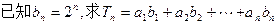 的值.
的值.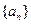 的前n项和
的前n项和 与通项
与通项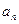 之间满足关系
之间满足关系
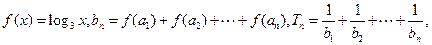 求
求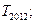
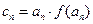 ,求
,求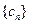 的前n项和
的前n项和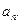
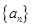 的公比
的公比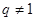 ,且
,且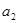 ,
,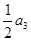 ,
,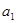 成等差数列,
成等差数列,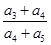 值是
值是 
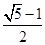

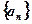
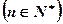 中,
中,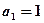 ,
,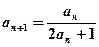 ,则
,则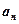 =
= 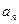 }中,
}中,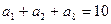 ,
,
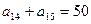 ,则此
,则此 数列的前15项之和是
数列的前15项之和是