题目内容
如图,AB是底面半径为1的圆柱的一条母线,O为下底面中心,BC是下底面的一条切线。
(1)求证:OB⊥AC;
(2)若AC与圆柱下底面所成的角为30°,OA=2。求三棱锥A-BOC的体积。
(1)见解析;(2)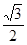 。
。
解析试题分析:(1)要证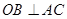 ,可转化为证OB⊥平面ABC,而根据圆的切线性质、圆柱母线定义可知
,可转化为证OB⊥平面ABC,而根据圆的切线性质、圆柱母线定义可知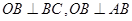 ,即OB⊥平面ABC;(2)三棱锥A-BOC的体积等于
,即OB⊥平面ABC;(2)三棱锥A-BOC的体积等于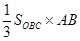 ,在RtΔOA B中,AB=
,在RtΔOA B中,AB=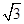 ,由题意知
,由题意知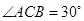 ,故
,故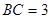 ,代入公式即可。
,代入公式即可。
试题解析: (1)连结OB,由圆的切线性质有OB⊥BC,圆柱母线性质有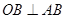 ,又
,又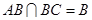 ,
,
∴OB⊥平面ABC,∴OB⊥AC。
(2)在RtΔOA B中,AB=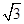 .
.
又∵∠ACB就是AC与底面⊙O所成角, ,
,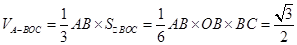
考点:(1)圆的切线性质、圆柱母线定义;(2)线面垂直判定及性质定理的应用;(3)三棱锥体积公式。

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
 的底面是直角三角形,
的底面是直角三角形, ,点
,点 在底面内的射影恰好是
在底面内的射影恰好是 的中点,且
的中点,且


 平面
平面 ;
; ,求点
,求点 到平面
到平面 的距离.
的距离. 中,
中, ,
, 平面
平面 ,
, ,
, 分别为
分别为 ,
, 的中点.
的中点.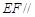 平面
平面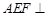 平面
平面 .
.
 .
. 时,求三棱锥F-DEG的体积V.
时,求三棱锥F-DEG的体积V.
 中,
中, ,
, ,
, ,
, ,点
,点 是
是 的中点.
的中点.
 ;
; 
 的体积.
的体积. 中,底面
中,底面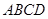 是平行四边形,
是平行四边形, ,
, 平面
平面 ,
, ,
, 是
是 的中点.
的中点. 平面
平面 ;
; 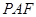 与平面
与平面 所成锐二面角的余弦值.
所成锐二面角的余弦值.
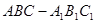 的底面为等腰直角三角形,
的底面为等腰直角三角形, ,
, ,
, 分别是
分别是 的中点。求异面直线
的中点。求异面直线 和
和 所成角的大小。
所成角的大小。
 的顶点均在同一个球面上,
的顶点均在同一个球面上, ,
, ,则
,则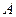 ,
, 两点间的球面距离为 .
两点间的球面距离为 .