题目内容
在同一坐标系中,方程
+
=1与ax+by2=0(a>b>0)的曲线大致是( )
| x2 |
| a2 |
| y2 |
| b2 |
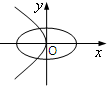
A、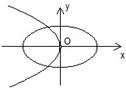 |
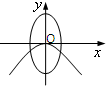
B、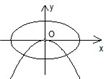 |
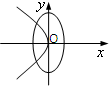
C、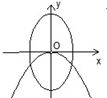 |
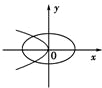
D、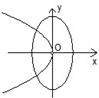 |
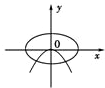
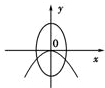
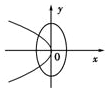
分析:先利用a>b判断出椭圆的焦点在x轴,故可排除C,D两项;整理抛物线的方程为标准方程可知其焦点在x轴,排除B项.答案可得.
解答:解:∵a>b
∴椭圆的焦点在x轴上,排除C和D,
整理抛物线方程得y2=-
x
∵a>b>0
∴-
<0
∴抛物线的开口向左,焦点在x轴.
故选A
∴椭圆的焦点在x轴上,排除C和D,
整理抛物线方程得y2=-
| a |
| b |
∵a>b>0
∴-
| a |
| b |
∴抛物线的开口向左,焦点在x轴.
故选A
点评:本题主要考查了椭圆和抛物线的简单性质,曲线与方程的问题.考查了学生对基础知识的掌握程度.

练习册系列答案
相关题目

 与
与 的曲线大致是(
)
的曲线大致是(
)