题目内容
在同一坐标系中,方程
+
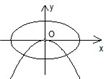
=1与bx2=-ay(a>b>0)表示的曲线大致是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、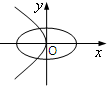 |
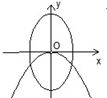
B、 |
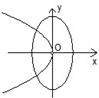
C、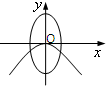 |
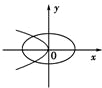
D、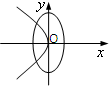 |
分析:根据题意,a>b>0,可以整理抛物线ax+by2=0变形为标准方程,结合椭圆
+
=1的形式,可以判断其焦点所在的位置,进而分析选项可得答案.
| x2 |
| a2 |
| y2 |
| b2 |
解答:解:由a>b>0,
椭圆a2x2+b2y2=1,即
+
=1,焦点在x轴上;
抛物线bx2=-ay,即y2=-
x,焦点在x轴的负半轴上;
分析可得,A符合,
故选A.
椭圆a2x2+b2y2=1,即
| x2 |
| a2 |
| y2 |
| b2 |
抛物线bx2=-ay,即y2=-
| a |
| b |
分析可得,A符合,
故选A.
点评:本题考查由椭圆、抛物线的方程判断图象的方法,注意先判断曲线的形状,再分析焦点等位置.

练习册系列答案
 小学课时作业全通练案系列答案
小学课时作业全通练案系列答案 金版课堂课时训练系列答案
金版课堂课时训练系列答案 单元全能练考卷系列答案
单元全能练考卷系列答案 新黄冈兵法密卷系列答案
新黄冈兵法密卷系列答案
相关题目
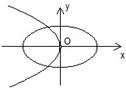
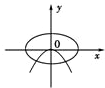
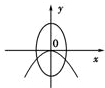
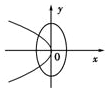
 与
与 的曲线大致是(
)
的曲线大致是(
)