题目内容
在同一坐标系中,方程
+
=1与y2=-
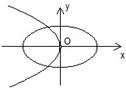
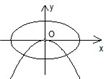
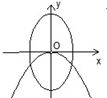
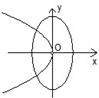
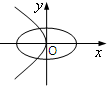
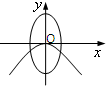
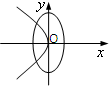
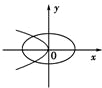
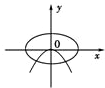
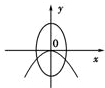
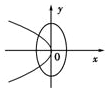
x(m>n>0)的曲线大致是( )
| x2 |
| n2 |
| y2 |
| m2 |
| m |
| n |
分析:根据m>n>0得到椭圆方程表示焦点在y轴上的椭圆,再由-
<0可得抛物线方程表示焦点在y轴上、开口向左的抛物线,由此对照各个选项可得本题答案.
| m |
| n |
解答:解:∵m>n>0,∴方程
+
=1表示曲线在y轴上的椭圆;
又∵-
<0,
∴抛物线y2=-
x表示焦点在x轴上的抛物线,顶点在原点且开口向左
由此对照各个选项,可得只有D项符合条件
故选:D
| x2 |
| n2 |
| y2 |
| m2 |
又∵-
| m |
| n |
∴抛物线y2=-
| m |
| n |
由此对照各个选项,可得只有D项符合条件
故选:D
点评:本题给出含有字母参数的圆锥曲线,判断两个曲线的大致位置,着重考查了椭圆、抛物线的标准方程和简单几何性质等知识,属于基础题.

练习册系列答案
相关题目

 与
与 的曲线大致是(
)
的曲线大致是(
)