题目内容
(本小题满分15分)
已知等比数列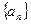 的前
的前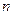 项和为
项和为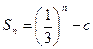 ,正数数列
,正数数列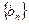 的首项为
的首项为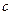 ,且满足:
,且满足: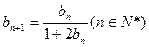 .记数列
.记数列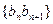 前
前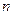 项和为
项和为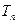 .
.
(Ⅰ)求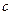 的值; (Ⅱ)求数列
的值; (Ⅱ)求数列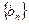 的通项公式;
的通项公式;
(Ⅲ)是否存在正整数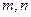 ,且
,且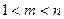 ,使得
,使得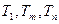 成等比数列?若存在,求出
成等比数列?若存在,求出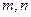 的值,若不存在,说明理由.
的值,若不存在,说明理由.
已知等比数列
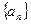 的前
的前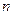 项和为
项和为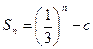 ,正数数列
,正数数列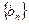 的首项为
的首项为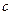 ,且满足:
,且满足: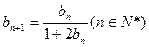 .记数列
.记数列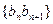 前
前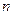 项和为
项和为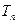 .
.(Ⅰ)求
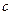 的值; (Ⅱ)求数列
的值; (Ⅱ)求数列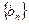 的通项公式;
的通项公式;(Ⅲ)是否存在正整数
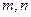 ,且
,且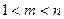 ,使得
,使得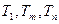 成等比数列?若存在,求出
成等比数列?若存在,求出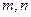 的值,若不存在,说明理由.
的值,若不存在,说明理由.(Ⅰ)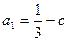 ,
,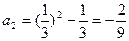 ,
,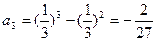 ………(3分)
………(3分)
因为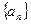 为等比数列所以
为等比数列所以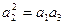 ,得
,得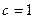 ………………………(4分)
………………………(4分)
经检验此时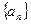 为等比数列. ………………(5分)
为等比数列. ………………(5分)
(Ⅱ)∵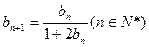 ∴
∴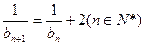
数列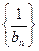 为等差数列 …………………………………………(7分)
为等差数列 …………………………………………(7分)
又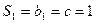 ,所以
,所以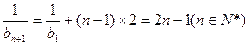
所以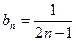
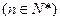 …………(10分)
…………(10分)
(Ⅲ)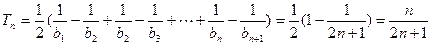 ……(12分)
……(12分)
假设存在正整数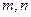 ,且
,且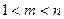 ,使得
,使得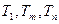 成等比数列
成等比数列
则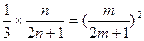 ,所以
,所以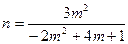
由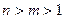 得
得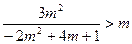 且
且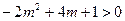
即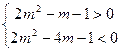 ,所以
,所以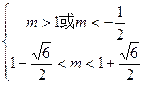
因为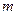 为正整数,所以
为正整数,所以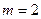 ,此时
,此时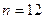
所以满足题意的正整数存在,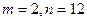 .…………(15分)
.…………(15分)
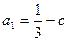 ,
,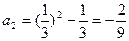 ,
,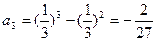 ………(3分)
………(3分)因为
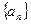 为等比数列所以
为等比数列所以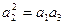 ,得
,得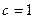 ………………………(4分)
………………………(4分) 经检验此时
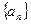 为等比数列. ………………(5分)
为等比数列. ………………(5分)(Ⅱ)∵
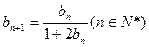 ∴
∴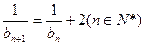
数列
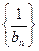 为等差数列 …………………………………………(7分)
为等差数列 …………………………………………(7分)又
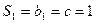 ,所以
,所以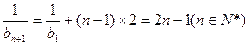
所以
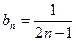
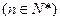 …………(10分)
…………(10分)(Ⅲ)
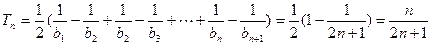 ……(12分)
……(12分)假设存在正整数
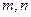 ,且
,且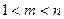 ,使得
,使得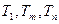 成等比数列
成等比数列则
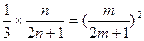 ,所以
,所以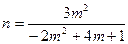
由
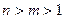 得
得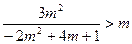 且
且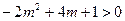
即
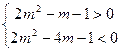 ,所以
,所以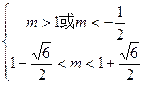
因为
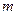 为正整数,所以
为正整数,所以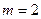 ,此时
,此时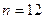
所以满足题意的正整数存在,
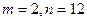 .…………(15分)
.…………(15分)略

练习册系列答案
相关题目
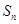 是等差数列
是等差数列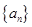 的前
的前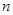 项和,已知
项和,已知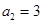 ,
,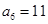 ,则
,则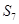 等于( )
等于( )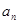 }中,
}中,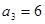 ,前三项和
,前三项和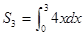 ,则公比
,则公比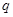 =( )
=( ) 
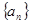 满足
满足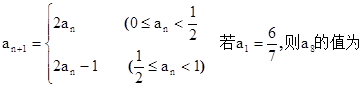 ( )
( )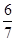
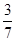
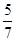
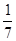
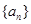 满足
满足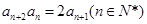 ,且
,且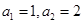 ,则数列
,则数列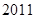 项的乘积为
项的乘积为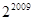
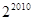
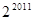
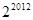
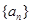 是等差数列,若
是等差数列,若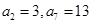 ,则数列
,则数列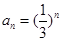 ,把数列
,把数列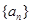 的各项同排成如下的三角形:记
的各项同排成如下的三角形:记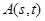 表示第s行的第t个数,则A(11,12)= ( )
表示第s行的第t个数,则A(11,12)= ( )




 中,
中, 则前11项的和
则前11项的和 = .
= .
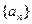 的前n项和为
的前n项和为 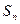 ,且
,且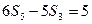 ,则
,则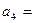 _________。
_________。