题目内容
若圆的方程为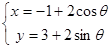 (
(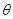 为参数),直线的方程为
为参数),直线的方程为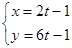 (t为参数),则直线与圆的位置关系是( )。
(t为参数),则直线与圆的位置关系是( )。
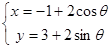 (
(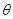 为参数),直线的方程为
为参数),直线的方程为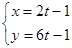 (t为参数),则直线与圆的位置关系是( )。
(t为参数),则直线与圆的位置关系是( )。| A.相交过圆心 | B.相交而不过圆心 | C.相切 | D.相离 |
B
试题分析:
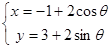 即
即 ,
,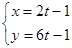 即
即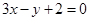 ,研究圆心(-1,3)到直线
,研究圆心(-1,3)到直线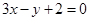 距离
距离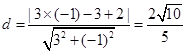 <2,所以,直线与圆的位置关系是相交而不过圆心,选B。
<2,所以,直线与圆的位置关系是相交而不过圆心,选B。点评:中档题,首先将参数方程转化成普通方程,利用几何法,研究关系。也可以利用代数法,研究方程组解的情况。

练习册系列答案
 数学奥赛暑假天天练南京大学出版社系列答案
数学奥赛暑假天天练南京大学出版社系列答案
相关题目
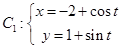 (
(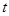 为参数),
为参数),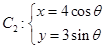 (
(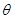 为参数).
为参数).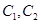 的方程为普通方程,并说明它们分别表示什么曲线;
的方程为普通方程,并说明它们分别表示什么曲线;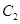 的左顶点且倾斜角为
的左顶点且倾斜角为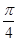 的直线
的直线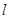 交曲线
交曲线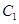 于
于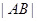 两点,求
两点,求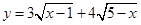 的最大值是 .
的最大值是 .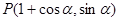 ,参数
,参数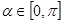
 ,点Q在曲线C:
,点Q在曲线C: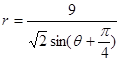 上.
上.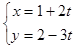 (
(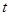 为参数),则直线的斜率为( )
为参数),则直线的斜率为( )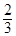
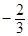
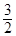
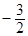
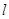 的参数方程为
的参数方程为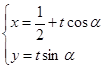
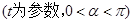 ,曲线
,曲线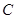 的极坐标方程为
的极坐标方程为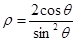 .
.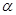 变化时,求
变化时,求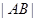 的最小值。
的最小值。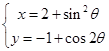 (
(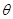 为参数)化成普通方程是
为参数)化成普通方程是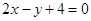

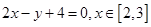
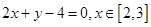
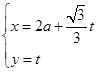 (
(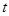 为参数,
为参数,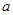 为常数且
为常数且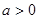 )被以原点为极点,
)被以原点为极点,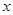 轴的正半轴为极轴,方程为
轴的正半轴为极轴,方程为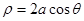 的曲线所截,求截得的弦长.
的曲线所截,求截得的弦长.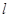 方程是
方程是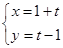
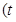 为参数),以坐标原点为极点,
为参数),以坐标原点为极点,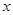 轴的正半轴为极轴建立极坐标系,圆
轴的正半轴为极轴建立极坐标系,圆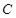 的极坐标方程为
的极坐标方程为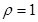 ,则圆
,则圆