题目内容
8.设A是双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1(a>0,b>0)在第一象限内的点,F为其右焦点,点A关于原点O的对称点为B,AF⊥BF,设∠ABF=$\frac{π}{6}$则双曲线离心率是$\sqrt{3}$+1.分析 确定△AOF是等边三角形,可得A($\frac{c}{2}$,$\frac{\sqrt{3}}{2}$c),代入双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{{c}^{2}}{4{a}^{2}}$-$\frac{3{c}^{2}}{4{b}^{2}}$=1,化简,即可求出双曲线离心率.
解答 解:∵点A关于原点O的对称点为B,
∴OA=OB,
∵AF⊥BF,∠ABF=$\frac{π}{6}$,
∴△AOF是等边三角形,
∴A($\frac{c}{2}$,$\frac{\sqrt{3}}{2}$c),
代入双曲线$\frac{{x}^{2}}{{a}^{2}}-\frac{{y}^{2}}{{b}^{2}}$=1,可得$\frac{{c}^{2}}{4{a}^{2}}$-$\frac{3{c}^{2}}{4{b}^{2}}$=1,
∴b2c2-3a2c2=4a2b2,
∴(c2-a2)c2-3a2c2=4a2(c2-a2),
∴e4-8e2+4=0,
∵e>1,∴e=$\sqrt{3}$+1.
故答案为:$\sqrt{3}$+1.
点评 本题考查双曲线离心率,考查双曲线方程的运用,确定A的坐标是关键.

练习册系列答案
相关题目
18.如图中的程序框图所描述的算法称为欧几里得辗转相除法.若输入m=459,n=357,则输出m=( )
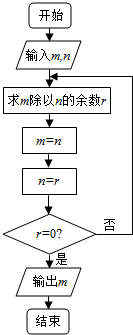

| A. | 51 | B. | 17 | C. | 9 | D. | 3 |
16.阅读如图所示的程序框图,运行相应的程序,则输出的结果s=( )
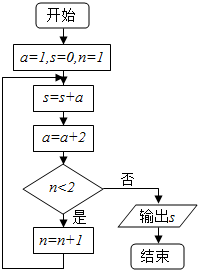

| A. | 0 | B. | 1 | C. | 3 | D. | 4 |
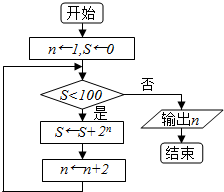
17.执行如图所示的程序框图(算法流程图),输出的n为( )


| A. | 3 | B. | 4 | C. | 5 | D. | 6 |
18.等比数列{an}的前n 项和为S n,若an>0,q>1,a3+a5=20,a2a6=64则公比q为( )
| A. | $\frac{1}{4}$ | B. | $\frac{1}{2}$ | C. | 2 | D. | 4 |
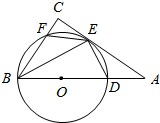 如图,△ABC是直角三角形,∠C为直角,D是斜边AB上一点,以BD为直径的圆O与AC相切于点E,与BC相交于点F.
如图,△ABC是直角三角形,∠C为直角,D是斜边AB上一点,以BD为直径的圆O与AC相切于点E,与BC相交于点F.